Exercícios sobre função bijetora
Uma função é classificada como bijetora se:
A) ela for injetora e não for sobrejetora.
B) ela for sobrejetora e não for injetora.
C) ela não for sobrejetora nem injetora.
D) ela for sobrejetora e injetora.
E) ela estiver domínio nos números reais.
Alternativa D
A função é bijetora se ela for injetora e sobrejetora simultaneamente.
Dada a função com domínio e contradomínio no conjunto dos números reais e lei de formação f(x) = 3x + 1, julgue as afirmativas a seguir:
I. A função f(x) é injetora.
II. A função f(x) é sobrejetora.
III. A função f(x) é bijetora.
Marque a alternativa correta:
A) somente a afirmativa I é verdadeira.
B) somente a afirmativa II é verdadeira.
C) somente a afirmativa III é verdadeira.
D) todas as afirmativas são falsas.
E) todas as afirmativas são verdadeiras.
Alternativa E
I. A função f(x) é injetora. (Verdadeiro)
Sabemos que essa função é injetora, pois valores diferentes possuem imagens diferentes.
II. A função f(x) é sobrejetora. (Verdadeiro)
A função também é sobrejetora, pois o contradomínio é o conjunto dos números reais, o conjunto imagem. Como o gráfico é uma reta, a imagem é igual ao contradomínio.
III. A função f(x) é bijetora. (Verdadeiro)
Como a função é sobrejetora e injetora, podemos concluir que ela é bijetora.
A função f: A→B é a função tal que \(f(x_1,x_2 )\) = x1+x2. Seja A = {-1, 0, 1, 2} e B = {-1, 0, 1, 2, 3}, podemos afirmar que essa função é:
A) bijetora, pois ela é sobrejetora e injetora.
B) não bijetora, pois ela é sobrejetora, mas não é injetora.
C) não bijetora, pois ela é injetora, mas não é sobrejetora.
D) não bijetora, pois ela não é injetora nem sobrejetora.
E) constante, pois, para todo x e y, o valor da imagem é sempre o mesmo.
F) inversível, pois ela admite inversa.
Alternativa B
Primeiro verificaremos se a função é injetora:
Sabemos que \(f(0,1)=0+1=1\) e que \(f(-1,2)=1\), logo, essa função não é injetora.
Agora verificaremos se a função é sobrejetora:
\(f(-1,0)=f(0,-1)=-1\)
\(f(1,0)=f(0,1)=1\)
\(f(2,0)=f(0,2)=2\)
\(f(-1,1)=f(1,-1)=0\)
\(f(-1,2)=f(2,-1)=1\)
\(f(1,0)=f(0,1)=1\)
\(f(1,2)=f(2,1)=3\)
Note que o contradomínio é igual à imagem da função, então essa função é sobrejetora. Como a função não é injetora, podemos afirmar que ela não é bijetora, pois é sobrejetora, mas não injetora.
Durante a aula de matemática, o professor construiu um diagrama para que os estudantes analisassem se a relação se tratava de uma função ou não:
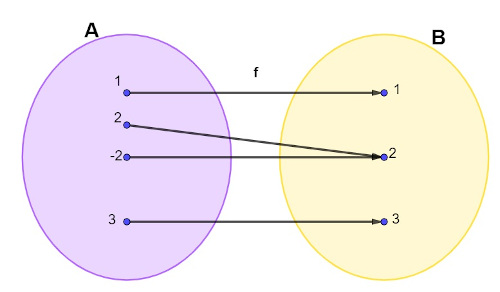
Após análise dos estudantes, o professor fez três afirmativas:
I. Essa relação é uma função.
II. Essa relação não é uma função bijetora.
III. Essa relação não é uma função injetora.
Utilizando V para verdadeiro e F para falso, as afirmativas I, II e III são, respectivamente:
A) V, V, V
B) V, V, F
C) V, F, V
D) F, F, V
E) F, V, F
Alternativa A
I. Essa relação é uma função. (Verdadeiro)
Note que para todo elemento de A existe um correspondente em B, logo, essa relação descreve uma função.
II. Essa relação não é uma função bijetora. (Verdadeiro)
De fato, essa relação não é uma bijeção, pois há um elemento no conjunto B que possui dois correspondentes em A.
III. Essa relação não é uma função injetora. (Verdadeiro)
Podemos perceber que \(f(2)=f(-2)\), o que faz com que a função não seja injetora.
Nos diagramas a seguir, há uma relação entre o conjunto A e o conjunto B.
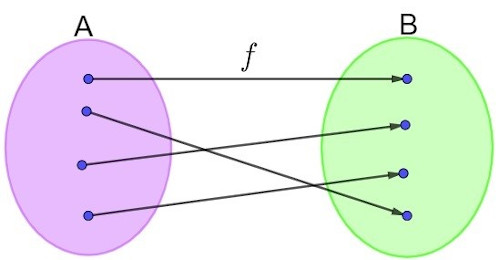
Sobre essa relação, podemos afirmar que:
A) a função f é injetora e não sobrejetora.
B) a função f é sobrejetora e não injetora.
C) a função f é bijetora.
D) a função f não admite inversa.
Alternativa C
Podemos observar que elementos distintos do conjunto A possuem imagem distinta, logo, essa função é injetora. A função também é sobrejetora, pois todos os elementos do conjunto B são correspondentes de, pelo menos, um elemento no conjunto A, como a função é sobrejetora e injetora, então ela é bijetora.
Uma função admite inversa quando
A) é injetora.
B) é sobrejetora.
C) é composta.
D) é bijetora.
E) é irracional.
Alternativa D
Uma função admite função inversa se for bijetora.
Analise o gráfico da função a seguir:
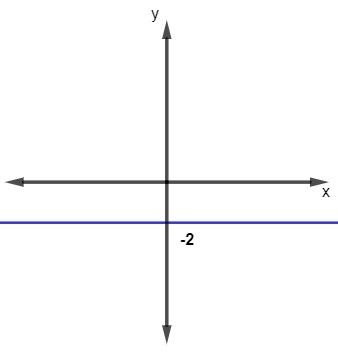
Se os números reais forem o domínio dessa função, e os números reais negativos forem o contradomínio, então podemos afirmar que:
A) essa função é bijetora.
B) essa função não é bijetora, pois ela é injetora e não é sobrejetora.
C) essa função não é bijetora, pois ela não é injetora e não é sobrejetora.
E) essa função não é bijetora, pois ela é sobrejetora e não é injetora.
Alternativa C
A função é a função constante com lei de formação f(x) = -2. Nesse caso, podemos observar que todos os elementos do domínio possuem mesma imagem, logo, essa função não é injetora, e observamos que a imagem é diferente do contradomínio, então ela não é sobrejetora. Assim, podemos concluir que a função não é bijetora, pois ela não é injetora e não é sobrejetora.
A função é inversível se ela é bijetora, ou seja, sobrejetora e injetora simultaneamente. Então, dada a função f: A → B, em que A: {1, 2, 3, 4} e B: {-2, 1, 6, 13}, com lei de formação f(x) = x² – 3, podemos afirmar que:
A) a função não é inversível, pois ela é injetora, mas não sobrejetora.
B) a função não é inversível, pois ela é sobrejetora, mas não injetora.
C) a função não é inversível, pois ela é bijetora.
D) a função é inversível, pois ela é bijetora.
Alternativa D
Analisando a função, verificaremos se ela é injetora e sobrejetora, então, primeiro, calcularemos a imagem de cada um dos valores do domínio:
f(1) = 1² – 3 = -2
f(2) = 2² – 3 = 4 – 3 = 1
f(3) = 3² – 3 = 9 – 3 = 6
f(4) = 4² – 3 = 16 – 3 = 13
Note que elementos diferentes do domínio sempre possuem imagens diferentes, e que o conjunto imagem é igual ao contradomínio da função, então essa função é injetora e sobrejetora, logo, ela é bijetora. Toda função bijetora é inversão, então a função é inversível, pois ela é bijetora.
O gráfico a seguir representa um recorte de um gráfico de uma função afim, conhecida também como função polinomial do 1º grau.
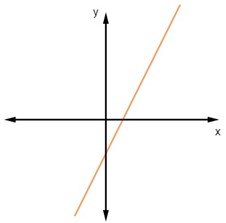
Analisando o gráfico dessa função, podemos afirmar que:
I. O gráfico dessa função para esse esboço é uma reta.
II. O gráfico mostra que, para esse intervalo, a função é bijetora.
III. A função afim é uma função inversível.
Marque a alternativa correta:
A) somente a afirmativa I é falsa.
B) somente a afirmativa II é salva.
C) somente a afirmativa III é falsa.
D) todas as afirmativas são falsas.
E) todas as afirmativas são verdadeiras.
Alternativa E
I. O gráfico dessa função para esse esboço é uma reta. (Verdadeiro)
O gráfico de uma função afim é sempre uma reta.
II. O gráfico mostra que, para esse intervalo, a função é bijetora. (Verdadeiro)
Note que a imagem é igual ao contradomínio da função, pois todos os elementos do eixo y são imagem de um elemento do eixo x. Note também que essa associação é única, ou seja, não existe um elemento do eixo y que é correspondente de mais de um elemento no eixo x, então essa função é bijetora.
III. A função afim é uma função inversível. (Verdadeiro)
Toda função bijetora é inversível, então essa função também é inversível.
Sabemos que f-1: B→A é uma função inversa, então podemos concluir que:
A) f: B→A é bijetora.
B) f: A→B é bijetora.
C) f: A→A é bijetora.
D) f-1:A→B é bijetora.
E) f-1B→B é bijetora.
Alternativa B
Uma função só admite inversa se ela for bijetora, a função f-1: B → A é a função inversa da função f : A → B, sendo assim, a função f : A → B é bijetora.
(IMA) Sobre funções injetoras, sobrejetoras e bijetoras, julgue os itens abaixo em verdadeiro ou falso.
I. Toda função injetora é bijetora.
II. Quando elementos diferentes geram imagens diferentes, temos uma função sobrejetora.
III. Toda função bijetora admite inversa.
VI. Quando a imagem é igual ao contradomínio, temos uma função sobrejetora.
A) VVVV
B) FFVV
C) VVFF
D) FFFF
Alternativa B
I. Toda função injetora é bijetora. (Falso)
Além de ser injetora, é necessário que a função seja sobrejetora também.
II. Quando elementos diferentes geram imagens diferentes, temos uma função sobrejetora. (Falso)
Essa é a característica da função injetora.
III. Toda função bijetora admite inversa. (Verdadeiro)
Uma função admite inversa se é bijetora.
VI. Quando a imagem é igual ao contradomínio, temos uma função sobrejetora. (Verdadeiro)
Para ser sobrejetora, a imagem tem que ser igual ao contradomínio.
(UFF) Considere as funções f, g e h, todas definidas em [m, n] com imagens em [p, q] representadas através dos gráficos a seguir.
![Gráficos das funções f, g e h, definidas em [m, n] com imagens em [p, q].](https://s2.static.brasilescola.uol.com.br/exercicios/2022/09/grafico-funcoes.png)
Pode-se afirmar que:
A) f é bijetiva, g é sobrejetiva e h não é injetiva.
B) f é sobrejetiva, g é injetiva e h não é sobrejetiva.
C) f não é injetiva, g é bijetiva e h é injetiva.
D) f é injetiva, g não é sobrejetiva e h é bijetiva.
E) f é sobrejetiva, g não é injetiva e h é sobrejetiva.
Alternativa A
Analisando os gráficos, podemos observar que:
- A função f é bijetiva, no domínio [m, n], pois todos os elementos do contradomínio [q, p] são imagens de um único elemento do domínio.
- No gráfico da função g, podemos observar que a função é sobrejetiva, pois o contradomínio é igual à imagem da função, entretanto, a função não é injetiva, pois há uma parte constante, em que elementos diferentes do domínio possuem a mesma imagem.
- No gráfico da função h, podemos observar que a função não é nem injetiva, nem sobrejetiva, pois a imagem é diferente do contradomínio, e há um momento em que a função é constante.
Então podemos afirmar que: f é bijetiva, g é sobrejetiva e h não é injetiva.
