Exercícios sobre Função Modular
Ao resolvermos exercícios sobre função modular, devemos atentar para as propriedades operatórias do módulo, bem como para as características de seu gráfico.
Publicado por: Amanda Gonçalves RibeiroQuestões
-
Questão 1
Se f(x) = x² + 2x e g(x) = |x³| + 2x, determine a composta de f com g e de g com f.
Primeiramente vamos encontrar a composição das funções f[g(x)]:
f(x) = x² + 2x
f[g(x)] = [g(x)]² + 2.[g(x)]
f[g(x)] = (|x³| + 2x)² + 2.(|– x³| + 2x)
f[g(x)] = |x³|² + 4x.|x³| + 4x² + 2.|x³| + 4x
f[g(x)] = |x|6 + 2.|x³| + 4x.(|x³| + x + 1)
Vamos agora determinar a composição das funções g[f(x)]:
g(x) = |x³| + 2x
g[f(x)] = |[f(x)]|³ + 2.[f(x)]
g[f(x)] = |x² + 2x|³ + 2.(x² + 2x)
g[f(x)] = |x|³.|x + 2|³ + 2x² + 4x
g[f(x)] = |x|6 + 6|x|5 + 12|x|4 + 8|x|3 + 2x² + 4x
-
Questão 2
Construa o gráfico da função modular f(x) = 2 + |x – 1|.
Para formular esse gráfico, podemos tomar como parâmetro o gráfico de f(x) = |x – 1|, que na imagem abaixo está retratado com a cor rosa. Esse gráfico toca o eixo x no ponto (1,0), pois |x – 1| = 0 se, e somente se, x = 1. Basta então “subir” o gráfico duas unidades. Dessa forma, podemos obter o gráfico de f(x) = 2 + |x – 1|, que na figura está representado com a cor vermelha:
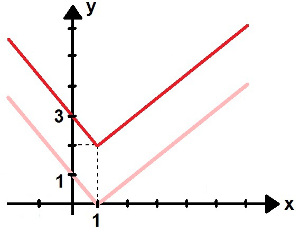
Gráfico da função modular f(x) = 2 + |x – 1| -
Questão 3
(UFSC) Sejam as funções f(x) = |x – 1| e g(x) = (x² + 4x – 4).
a) Inicialmente vamos realizar a composição das funções f[g(x)].
f(x) = |x – 1|
f[g(x)] = |g(x) – 1|
f[g(x)] = |(x² + 4x – 4) – 1|
f[g(x)] = |x² + 4x – 5|Para determinar as raízes da equação f[g(x)] = 0, utilizaremos a fórmula de Bhaskara:
.jpg)
Δ = 4² – 4.1.(– 5)
Δ = 16 + 20
Δ = 36x = – 4 ± √36
2.1x = – 4 ± 6
2x = – 2 ± 3
x' = – 2 + 3 = 1
x'' = – 2 – 3 = – 5As raízes de f[g(x)] são 1 e – 5.
b) Se desconsiderarmos que se trata de uma função modular, podemos analisar que a função f[g(x)]1 = x² + 4x – 5 corresponde ao gráfico de uma parábola com concavidade para cima. Através dos cálculos de máximo e mínimo de uma parábola, podemos determinar as coordenadas do vértice:
Xv = – b
2aXv = – 4
2.1Xv = – 2
Yv = – Δ
4aYv = – 36
4.1Yv = – 9
Portanto, o vértice da parábola de f[g(x)]1 é o ponto (– 2, – 9). Mas como estamos trabalhando com uma função modular, a parte da parábola que se encontra no 3° quadrante, isto é, os valores de f[g(x)] < 0, é refletida no 2° quadrante. Na imagem a seguir temos o gráfico correspondente à função f[g(x)]. Observe que, em vermelho, temos a curva assumida pelo gráfico da função modular, já, em rosa, temos a curva da função caso esta não fosse modular:
![Gráfico da função modular f[g(x)] = |x² + 4x – 5|](https://s1.static.brasilescola.uol.com.br/img/2014/09/questao3-funcao-modular.jpg "Questão 3 – Função modular")
Gráfico da função modular f[g(x)] = |x² + 4x – 5| -
Questão 4
(UFF – RJ) Considere a função f definida por
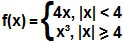. Pede-se:a) O módulo de zero é o próprio zero, portanto, é menor do que 4. Sendo assim, usaremos a lei da função: f(x) = 4x. Para x = 0, temos:
f(x) = 4x
f(0) = 4.0
f(0) = 0Sendo assim, temos f(0) = 0.
b) Vamos calcular primeiro o valor de f(– 2). Como |– 2| < 4, utilizaremos f(x) = 4x:
f(x) = 4x
f(– 2) = 4.(– 2)
f(– 2) = – 8Agora calcularemos a composição (f o f) (– 2) que corresponde a f(f(– 2)) = f(– 8). Como |– 8| ≥ 4, utilizaremos f(x) = x³:
f(x) = x³
(f o f) (– 2) = (– 8)³
(f o f) (– 2) = – 512Portanto, (f o f) (– 2) = – 512.
c) O valor de f(m) = – 125 só pode corresponder a uma das leis da função. Mas como – 125 não é múltiplo de 4, a função não pode ser f(x) = 4x. Sendo assim, utilizaremos a função f(x) = x³:
f(x) = x³
– 125 = x³
x =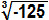
x = – 5d) Como |¼| < 4, utilizaremos f(x) = 4x:
f–1(¼) = a
f(a) = ¼
4a = ¼
a = 1
16Temos então que f–1(¼) = 1/16.