Exercícios sobre média geométrica
Faça estes exercícios sobre média geométrica, que, com a média harmônica e a média aritmética, faz parte das médias pitagóricas.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Uma piscina no formato de um prisma retangular possui 2 metros de profundidade, 6 metros de largura e 18 metros de comprimento. Se fosse construído um reservatório no formato de um cubo que tivesse o mesmo volume da piscina, a medida das suas arestas seria de:
A) 4 metros
B) 5 metros
C) 6 metros
D) 7 metros
E) 8 metros
Alternativa C
Para calcular a medida da aresta do cubo, basta calcular a média geométrica entre as medidas da piscina:
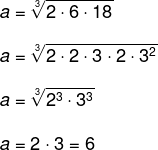
-
Questão 2
A média geométrica entre os números 10, 16, 25, 45, 135 é igual a:
A) 18
B) 25
C) 28
D) 30
E) 35
Alternativa D
Calculando a média geométrica, temos que:
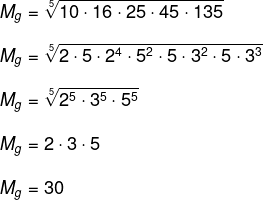
-
Questão 3
Para manter o controle de produção de uma indústria, os funcionários contam a quantidade de peças defeituosas produzidas ao longo dos dias da semana e calculam a diferença entre a média aritmética e a média geométrica do total dessas peças.
Em uma determinada semana, de segunda a sexta, o número de defeitos registrados foram, nesta ordem, 8, 16, 27, 18, 4. Então, a diferença entre a média arimética e a média geométrica nessa semana foi de:
A) 3,0
B) 2,9
C) 2,8
D) 2,7
E) 2,6
Alternativa E
Primeiro calcularemos a média arimética:
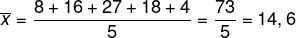
Agora vamos calcular a média geométrica:
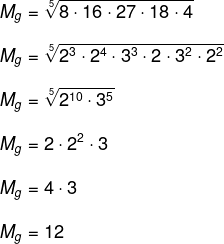
Então, a diferença entre a média aritmética e a média geométrica foi de: 14,6 – 12 = 2,6.
-
Questão 4
A média geométrica entre os números n, 2, 12 e 18 é igual a 6, então, o valor de n é igual a:
A) 10
B) 7
C) 6
D) 3
E) 2
Alternativa D
Calculando a média geométrica, temos que:
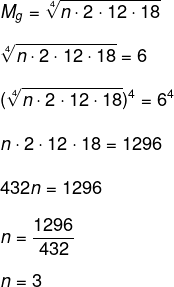
-
Questão 5
A população de certa cultura de bactérias se reproduz como uma progressão geométrica, conforme a sequência a seguir, em que x é o número de bactérias em milhões.
B = {x, x + 4, 9x}
Analisando essa progressão, o valor de x, em milhões, é:
A) 0,1 milhão de bactérias.
B) 0,5 milhão de bactérias.
C) 1 milhão de bactérias.
D) 2 milhões de bactérias.
E) 3 milhões de bactérias.
Alternativa D
Em uma progressão geométrica, sabemos que a média geométrica das extremidades é igual ao termo central. Então, temos que:
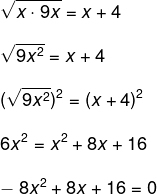
Agora queremos encontrar os zeros da equação, e, para isso, podemos simplificar, dividindo toda a equação por 8, então, temos que:
-8x² + 8x + 16 = 0 (: 8)
-x² + x + 2 = 0
Calculando delta, temos que:
a = -1, b = 1 e c = 2
Δ = b² – 4ac
Δ = 1² – 4(-1)2
Δ = 1 + 8
Δ = 9
Agora, pela fórmula de Bháskara, temos que:
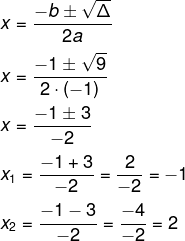
Analisando as soluções, é impossível que a quantidade de bactérias seja negativa, logo, havia 2 milhões de bactérias inicialmente.
-
Questão 6
Em uma escola, ao decorrer do bimestre, o estudante recebe 4 notas distintas de 0 a 10. São elas: a nota da prova, a nota do simulado, a nota das atividades em sala de aula e a nota do seminário. Para calcular a média bimestral na escola, calcula-se a média geométrica entre essas 4 notas. Veja o quadro, a seguir, com a nota de dois alunos:
Alunos
Prova
Simulado
Atividades
Seminário
Paulo
8
4
5
9
Renato
6
7
8
4
Ao calcular a média do boletim desses estudantes, podemos afirmar que:A) Paulo obteve uma nota maior que a do Renato.
B) Paulo obteve uma nota menor que a do Renato.
C) As notas de Paulo e Renato são as mesmas.
D) Ambos tiraram nota abaixo de 6 pontos no bimestre.
Alternativa A
Primeiro calcularemos a média geométrica das notas de cada aluno, começando pelas notas do Paulo:
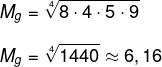
Agora calcularemos a média geométrica das notas de Renato:
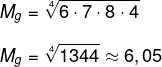
É possível perceber, então, que a média geométrica das notas de Paulo é maior do que a média geométrica das notas de Renato.
-
Questão 7
Durante a campanha de uma empresa para o Dia do Irmão, cada um dos membros da sala de marketing colocou o número de irmãos que possui na lista a seguir: {2, 1, 4, 2}. A média geométrica da quantidade de irmãos dos funcionários é:
A) 2,25
B) 1,75
C) 2,0
D) 2,4
E) 2,5
Alternativa C
Calculando a média geométrica, temos que:
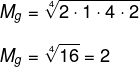
-
Questão 8
A inflação é um termo da economia frequentemente utilizado para designar o aumento geral dos preços na sociedade. Ela representa o aumento do custo de vida para o consumidor e para as empresas, resultante da elevação do preço dos produtos e da desvalorização da moeda. Quando notamos que alguns produtos são mais caros hoje do que eram antes, significa que o seu preço inflacionou. Normalmente, esse processo não costuma ser prejudicial para o consumidor, pois os reajustes nos salários-mínimos visam, sobretudo, ao acompanhamento das taxas de inflação.
PENA, Rodolfo F. Alves. O que é inflação? Brasil Escola. Disponível em: https://brasilescola.uol.com.br/o-que-e/geografia/o-que-e-inflacao.htm.
Nos anos de 2020, 2019 e 2018, a inflação foi de, respectivamente, 5%, 4% e 6%. Então, o valor médio de inflação nesses anos foi de, aproximadamente:
A) 3,8%
B) 4,9%
C) 5,0%
D) 5,1%
E) 6,0
Alternativa B
Para encontrar o valor médio da inflação por ano, calcularemos a média geométrica entre os valores das porcentagens. Passando para forma decimal, temos:
Aumento de 5% → 1,05
Aumento de 4% → 1,04
Aumento de 6% → 1,06
Agora, calcularemos a média geométrica:
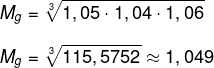
Logo, o valor médio foi de 4,9%.
-
Questão 9
(Cespe – adaptado) Considerando que a estatística reúne importantes ferramentas para a análise e a interpretação de dados, julgue o item a seguir.
Considere as séries X = {2, 6, 30} e Y = {5, 6, 12} e julgue as afirmativas abaixo:
I - possuem a mesma média geométrica.
II - possuem a mesma mediana.
III - a diferença entre as médias geométrica e aritmética será maior na série X.
Estão corretas:
A) Somente a afirmativa I
B) Somente a afirmativa II
C) Somente a afirmativa III
D) Somente as afirmativas I e II
E) Todas as afirmativas
Alternativa E
Verificando a afirmativa I, calcularemos a média geométrica dos dois conjuntos:
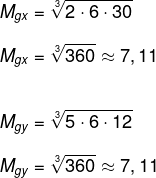
A afirmativa I é verdadeira, pois a média geométrica é a mesma.
Agora, verificando a afirmativa II, é possível perceber que o termo central tanto do conjunto X quanto do conjunto Y é o 6, que é a mediana, então, as medianas são iguais. A afirmativa II é verdadeira.
Por fim, cercaremos a afirmativa III. Para isso é necessário calcular a média aritmética de cada um dos conjuntos.
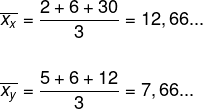
A média geométrica do conjunto X e do conjunto Y é, aproximadamente, 7,11. Então, a diferença entre a média geométrica e a aritmética do conjunto X é maior que a diferença entre a média geometria e a aritmética do conjunto Y.
A afirmativa III também é verdadeira.
-
Questão 10
(FCC) Considere as seguintes informações:
I. (A) = média harmônica dos números 4, 6 e 12.
II. (B) = média geométrica dos números 4, 6 e 12.
A média aritmética de (A) + (B) é igual a
A) 6,81.
B) 5,68.
C) 6,30.
D) 5,41.
E) 6,93.
Primeiro calcularemos a média harmônica entre 4,6 e 12:
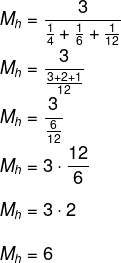
Agora, calcularemos a média geométrica entre os mesmos números:
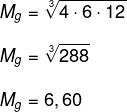
Por fim, calcularemos a média aritmética entre os resultados encontrados:
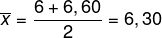
-
Questão 11
Certo investimento teve oscilações durante o mês. Na primeira semana, ele teve um aumento de 5%. Já na segunda semana, houve uma queda de 3%. Por fim, na terceira e quarta semanas houve, respetivamente, aumento de 15% e de 2%. Sendo assim, a média geométrica dessa oscilação é de um aumento de, aproximadamente:
A) 5%
B) 4,8%
C) 4,5%
D) 3,9%
E) 3,3%
Alternativa C
Primeiro representaremos de forma percentual:
Aumento de 5% = 1,05
Queda de 3% = 0,97
Aumento de 15% = 1,15
Aumento de 2% = 1,02
Calculando a média geométrica, temos que:
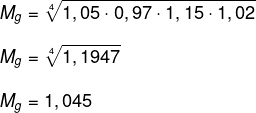
A média percentual é um aumento de 4,5%.
-
Questão 12
Ao longo do ano, a gasolina sofreu reajustes sucessíveis. O primeiro deles foi um aumento de 8%, o segundo, de 12%, e o terceiro, de 15%, então, a taxa média de reajuste foi de:
A) 9,52%
B) 9,98%
C) 10,28%
D)10,54%
E) 11,63%
Alternativa E
Calcularemos a média geométrica entre:
Aumento de 8% → 1,08
Aumento de 12% → 1,12
Aumento de 15% → 1,15
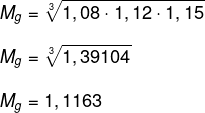
Houve um aumento médio de 11,63%.