Exercícios sobre produtos notáveis
Esta lista de exercícios sobre produtos notáveis tem como objetivo testar seus conhecimentos sobre essas simplificações de produtos algébricos.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Analisando as alternativas a seguir, marque aquela que contém de forma correta a solução do produto notável (x – 5)²:
A) x² + 25
B) x² – 25
C) x² – 10x + 25
D) x² + 10x – 25
E) x² + 10
Alternativa C
Note que estamos calculando o quadrado de uma diferença. Nesse produto notável, temos como resposta:
(x – 5)² = x² – 2 · 5 · x + 5²
(x – 5)² = x² – 10x + 25
-
Questão 2
Durante as aulas de matemática, o professor Raul decidiu revisar com os estudantes os produtos notáveis. Então, ele escreveu no quadro as seguintes expressões:
I → (x – 2) (x + 2)
II → (x + 3)²
III → (x – 2)³
Os produtos notáveis listados pelo professor são conhecidos, respectivamente, como:
A) Quadrado da diferença, quadrado da soma e cubo da diferença.
B) Produto da soma pela diferença, quadrado da soma e cubo da diferença.
C) Trinômio quadrado perfeito, cubo da soma, cubo da diferença.
D) Quadrado da soma, produto da soma pela diferença e cubo da diferença.
E) Produto da soma pela diferença, quadrado do cubo, cubo da diferença.
-
Questão 3
Realizando a simplificação da expressão algébrica a seguir, encontraremos:
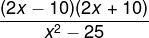
A) 1
B) 2
C) 3
D) 4
E) 5
Alternativa D
Podemos observar que, no numerador, temos um produto da soma pela diferença, então, temos que:
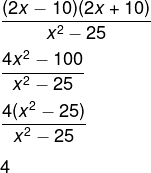
-
Questão 4
Simplificando a expressão (x + 5)² – x (x + 10), encontraremos:
A) 25
B) 30
C) 50
D) 75
E) 100
Alternativa A
Calculando, temos que:
(x + 5)² – x(x + 10)
x² + 10x + 25 – x² – 10x
25
-
Questão 5
Resolvendo os produtos notáveis da expressão (2x – 5) (2x + 5) – (2x – 5)² e simplificando, encontraremos como resultado o polinômio:
A) 20x
B) 20x – 50
C) 8x³ + 2x²
D) 50
E) 2x – 25
Alternativa B
Resolvendo os produtos notáveis, temos que:
(2x – 5) (2x + 5) – (2x – 5)²
4x² – 25 – (4x² – 20x + 25)
4x² – 25 – 4x² + 20x – 25
20x – 50
-
Questão 6
Durante os estudos de cálculo 1, um matemático se deparou com a seguinte expressão: (g + a) (g – a), vendo-se diante de um produto notável conhecido como o produto da soma pela diferença. A solução desse produto notável é sempre igual ao:
A) quadrado do primeiro termo, mais duas vezes o primeiro, vezes o segundo termo, mais o quadrado do segundo termo.
B) quadrado do primeiro termo, menos duas vezes o primeiro, vezes o segundo termo, mais o quadrado do segundo termo.
C) quadrado do primeiro termo menos o segundo termo.
D) quadrado do primeiro termo mais o quadrado do segundo termo.
E) quadrado do primeiro termo menos o quadrado do segundo termo.
Alternativa D
Temos um caso de produto da soma pela diferença, que tem como resposta o quadrado do primeiro termo menos o quadrado do segundo termo.
-
Questão 7
Ao desenvolver o produto (2x + 4)², encontramos como solução o polinômio:
A) 4x² + 16x + 16
B) 4x + 16
C) 4x² + 16
D) 2x² + 8x + 8
E) 4x + 8
Alternativa A
Calculando o produto notável conhecido como quadrado da soma, temos como resultado:
(2x + 4)² = 4x² + 16x + 16
-
Questão 8
Das alternativas a seguir, marque aquela que contém um produto notável:
A) x² + 25
B) (x² – 3)
C) (a – 3)²
D) (x + 2) (x – 4)
E) (x – 1) (x – 2) (x + 3)
Alternativa C
Note que, na alternativa C, temos o cubo da diferença, que é um produto notável; as demais não são produtos notáveis.
-
Questão 9
Sobre os produtos notáveis, julgue as afirmativas a seguir:
I → A multiplicação de dois polinômios é sempre um produto notável.
II → O produto (a + b)³ é um produto notável.
III → O produto da soma pela diferença é sempre igual à soma do quadrado do primeiro e segundo termos.
Marque a alternativa correta:
A) Somente a afirmativa I é falsa.
B) Somente a afirmativa II é falsa.
C) Somente a afirmativa III é falsa.
D) Todas as afirmativas são falsas.
E) Todas as afirmativas são verdadeiras.
Alternativa A
I → A multiplicação de dois polinômios é sempre um produto notável. (falsa)
Nem sempre uma multiplicação é um produto notável.
II → O produto (a + b)³ é um produto notável. (verdadeiro)
Verdadeira, pois trata-se do cubo da soma.
III → O produto da soma pela diferença é sempre igual à soma do quadrado do primeiro e segundo termos. (verdadeira)
Sempre que encontramos um produto da soma pela diferença, ele será igual ao quadrado do primeiro termo menos o quadrado do segundo termo.
-
Questão 10
(UFRGS 2016) Se x + y = 13 e x · y = 1, então, x² + y² é:
A) 166
B) 167
C) 168
D) 169
E) 170
Alternativa B
Calculando o quadrado da soma, temos que:
(x + y)² = x² + 2xy + y²
Sabemos que x + y = 13 e que xy = 1:
(13)² = x² + 2 · 1 + y²
169 = x² + 2 + y²
169 – 2 = x² + y²
167 = x² + y²
-
Questão 11
A diferença entre (1522² – 1520²) é igual a:
A) 2000
B) 2340
C) 5040
D) 6084
E) 7320
Alternativa D
Transformando essa operação em um produto da soma pela diferença, temos que:
(1522 + 1520) (1522 – 1520)
34420 · 2
6084
-
Questão 12
(IMNEC) A diferença entre o quadrado da soma e o quadrado da diferença entre dois números reais é igual:
A) à diferença dos quadrados dos dois números.
B) à soma dos quadrados dos dois números.
C) à diferença dos dois números.
D) ao dobro do produto dos números.
E) ao quádruplo do produto dos números.
Alternativa E
Seja a e b dois números, sabemos que:
(a + b)² =a² + 2ab + b²
Por outro lado, o quadrado da diferença é dado por:
(a – b)² = a² – 2ab + b²
Então, queremos a diferença do quadrado da soma e o quadrado da diferença:
a² + 2ab + b² – (a² – 2ab + b²)
a² + 2ab + b² – a² + 2ab – b²
4ab