Exercícios sobre Prisma
Teste os seus conhecimentos: Faça exercícios sobre Prismae veja a resolução comentada.
Publicado por: Marcos Noé Pedro da SilvaQuestões
-
Questão 1
Qual o volume de concreto utilizado na construção de uma laje de 80 centímetros de espessura em uma sala com medidas iguais a 4 metros de largura e 6 metros de comprimento?
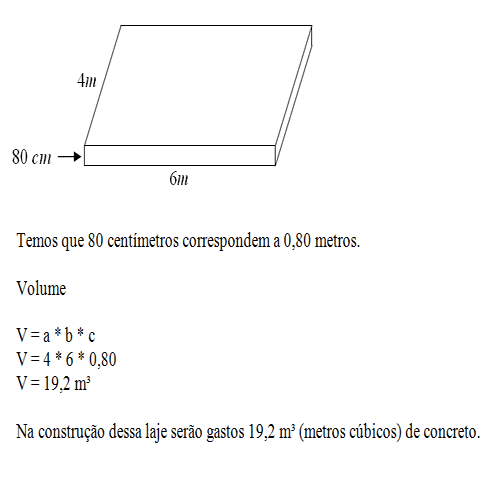
-
Questão 2
Um prisma de base quadrangular possui volume igual a 192 cm³. Determine sua altura sabendo que ela corresponde ao triplo da medida da aresta da base.
Aresta da base: x cm
Altura: 3x cm
Volume: 192V = x * x * 3x
3x³ = 192
x³ = 192/3
x³ = 64
x = 4Altura: 3 * 4 = 12 cm
A altura do prisma de base é correspondente a 12 cm.
-
Questão 3
Uma caixa de papelão será fabricada por uma indústria com as seguintes medidas: 40 cm de comprimento, 20 cm de largura e 15 cm de altura. Essa caixa irá armazenar doces na forma de um prisma com as dimensões medindo 8 cm de comprimento, 4 cm de largura e 3 cm de altura. Qual o número de doces necessários para o preenchimento total da caixa fabricada?
Volume da caixa
V = 40 * 20 * 15
V = 12000 cm³Volume do doce
V = 8 * 4 * 3
V = 96 cm³Número total de doces armazenados na caixa
12000 / 96 = 125Serão armazenadas 125 barras de doces na caixa com as dimensões fornecidas.
-
Questão 4
(UFOP–MG)
A área total de um cubo cuja diagonal mede 5√3 cm é:
a) 140 cm²
b) 150 cm²
c) 120√2 cm²
d) 100√3 cm²
e) 450 cm²
A diagonal de um cubo pode ser calculada através da seguinte expressão matemática:
d = a√3. Foi fornecido que a medida da diagonal do cubo é 5√3, então: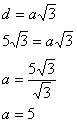
A medida da aresta desse cubo mede 5 cm. Dessa forma, cada face do cubo medirá:
A = 5 * 5
A = 25 cm²Sabendo que o cubo possui 6 faces laterais temos:
Área Total: 6 * 25
Área Total: 150 cm²A área total do cubo com diagonal medindo 5√3 cm é igual a 150 cm².
Resposta correta: item b.
-
Questão 5
(FEI–SP)
As medidas das arestas de um paralelepípedo retângulo são proporcionais a 2, 3 e 4. Se sua diagonal mede 2√29 cm, seu volume, em centímetros cúbicos, é:
a) 24
b) 24√29
c) 116
d) 164
e) 192


-
Questão 6
(FGV–SP)
Em uma piscina retangular com 10 m de comprimento e 5 m de largura, para elevar o nível de água em 10 cm são necessários:
a) 500 l de água
b) 5 000 l de água
c) 10 000 l de água
d) 1 000 l de água
e) 50 000 l de água
A medida correspondente a 10 cm forma um paralelepípedo de medidas 10 m, 5 m e 10 cm. Transformando 10 cm em metros temos 0,1. Dessa forma:
V = 10 * 5 * 0,1
V = 5 m³
V = 5000 litrosResposta correta: item b.