Exercícios sobre raiz quadrada
Esta lista de exercícios aborda raiz quadrada, que é a operação inversa da potência. Para calculá-la, devemos encontrar qual número que, elevado ao quadrado, é igual ao radicando.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Um terreno possui área igual a 196 m². Sabendo que esse terreno tem formato de um quadrado, então os seus lados possuem medida igual a:
A) 12 m.
B) 13 m.
C) 14 m.
D) 15 m.
E) 16 m.
Alternativa C.
A área de um quadrado é igual ao lado ao quadrado, então, para encontrar o valor do lado, vamos calcular a raiz quadrada da área do terreno.
Para calcular a raiz quadrada de 196, vamos fatorar esse número:
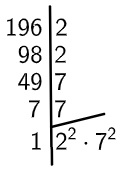
Então, temos que:
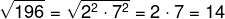
-
Questão 2
Dos números abaixo, marque aquele que possui uma raiz quadrada exata.
A) 600
B) 215
C) 144
D) 110
E) 70
Alternativa C.
Analisando as alternativas, a única que é formada por um quadrado perfeito é a alternativa “c”, pois temos que 12² = 144, ou seja, √144 = 12. As demais alternativas não são raízes exatas.
-
Questão 3
O valor da expressão algébrica a seguir é:
√4+√16 – √25 ×√9
A) – 9.
B) – 6.
C) – 5.
D) – 4.
E) – 2.
Alternativa A.
Resolvendo a expressão, temos que:
√4+√16 – √25 ×√9
2 + 4 – 5 × 3
6 – 15
– 9 -
Questão 4
(Cefet/RJ 2014) Por qual número devemos multiplicar o número 0,75 de modo que a raiz quadrada do produto obtido seja igual a 45?
A) 2700
B) 2800
C) 2900
D) 3000
Alternativa A.
Seja x o número procurado, temos que:
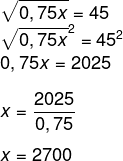
-
Questão 5
O valor da expressão numérica a seguir é:
A) 2
B) 3
C) 4
D) 5
E) 6
Alternativa A.
Realizando o produto, temos que:
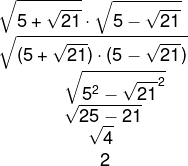
-
Questão 6
Qual é a raiz quadrada de 5184?
A) 42
B) 58
C) 68
D) 72
E) 88
Alternativa D.
Fatorando 5184, temos que:

Então, podemos fazer o seguinte cálculo:
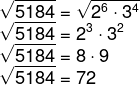
-
Questão 7
Analise as afirmativas a seguir:
I - A raiz quadrada de 1500 é menor que 38.
II – A raiz quadrada de 190 é maior que 13.
III – A raiz quadrada de 0 é igual a 0.
Marque a alternativa correta.
A) Somente a afirmativa I é verdadeira.
B) Somente a afirmativa II é verdadeira.
C) Somente a afirmativa III é verdadeira.
D) Somente as afirmativas I e II são verdadeiras.
E) Somente as afirmativas II e III são verdadeiras.
Alternativa E.
I → Falsa, pois sabemos que 38 · 38 = 1.444, logo a raiz de 1500 é maior que 38.
II → Verdadeira, pois sabemos que 13 · 13 = 169, logo a raiz de 190 é maior que 13.
III → Verdadeira, pois a raiz de 0 é 0.
-
Questão 8
(Ethos concursos) A raiz quadrada de um número é uma importante operação matemática, assim como a adição, a subtração, a multiplicação e a divisão. Somente alguns números possuem raiz quadrada, são aqueles considerados quadrados perfeitos. Sendo assim, calcule a raiz quadrada de 625 e assinale a alternativa CORRETA.
A) 35
B) 24
C) 25
D) 17
E) 49
Alternativa C.
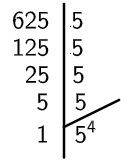
Então, temos que:
√625 = √54
√625 = 5²
√625 = 25 -
Questão 9
Qual é o valor da simplificação da expressão a seguir?
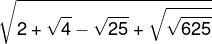
A) 0
B) 1
C) 2
D) 3
E) 4
Alternativa C.
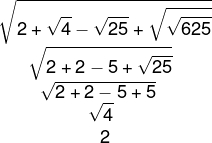
-
Questão 10
Sabendo que √x = 9, então o valor da terça parte de x é:
A) 81
B) 72
C) 36
D) 27
E) 9
Alternativa D.
√x = 9
√x² = 9²
x = 81Como queremos a terça parte de x então 81: 3 = 27.
-
Questão 11
Sobre a raiz quadrada, julgue as afirmativas a seguir.
I → Não é possível calcular a raiz quadrada de número negativo.
II → Os números 0, 1, 4, 9 e 16 são todos os quadrados perfeitos menores que 20.
III → A raiz quadrada de 8 é igual a 4.
As afirmativas são, respectivamente:
A) V, V e V.
B) F, F e F.
C) F, F e V.
D) V, V e F.
E) V, F e V.
Alternativa D.
I → Verdadeira.
II → Verdadeira.
II → Falsa, pois 4 é raiz quadrada de 16, e não de 8.
-
Questão 12
(IFG 2019) Os babilônicos talvez tenham usado a fórmula abaixo para obter aproximações interessantes de raízes quadradas de números não quadrados perfeitos.
Atribuindo a = 4/3 e b = 2/9 nessa fórmula, é correto afirmar que obtemos a aproximação:
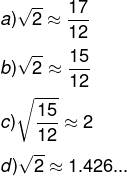
Alternativa a.
Vamos substituir o valor de a e b: