Exercícios sobre redução ao primeiro quadrante
Para resolver estes exercícios sobre redução ao primeiro quadrante, é necessário saber estabelecer comparações entre os ângulos correspondentes do ciclo trigonométrico.
Publicado por: Amanda Gonçalves RibeiroQuestões
-
Questão 1
Reduza ao 1° quadrante o ângulo de 150°.
Seja x o correspondente, no primeiro quadrante, do ângulo de 150°, que está no 2° quadrante. Para reduzi-lo ao primeiro quadrante do ciclo trigonométrico, faremos:
180° – x = 150°
– x = 150° – 180°
– x = – 30°
x = 30°Portanto, o ângulo de 30° é correspondente a 150°.
-
Questão 2
Reduza ao 1° quadrante o ângulo de 310°.
Chamemos de x o ângulo do primeiro quadrante que é correspondente a 310°, um ângulo situado no 4° quadrante.
360° – x = 310°
– x = 310° – 360°
– x = – 50°
x = 50°O ângulo de 50° é o correspondente de 310° no primeiro quadrante.
-
Questão 3
Reduza ao 1° quadrante o ângulo de 4π/3.
Vamos chamar de x o ângulo do primeiro quadrante que é correspondente a 4π/3, um ângulo do 3° quadrante.
π + x = 4π
3x = 4π – π
3x = 4π – 3π
3x = π
3Logo, o ângulo de π/3 é o correspondente de 4π/3 no primeiro quadrante.
-
Questão 4
(UFRGS) Considere as afirmações a seguir:
I. tan 92° = –tan 88°
II. tan 178° = tan 88°
III. tan 268° = tan 88°
IV. tan 272° = –tan 88°
Quais estão corretas?
a) I, III
b) III, IV
c) I, II, IV
d) I, III, IV
e) II, III, IV
De acordo com a figura a seguir, podemos constatar qual é o sinal da tangente de um ângulo a depender do quadrante em que ele se encontra. Ângulos situados no 1° e no 3° quadrante possuem tangente positiva, enquanto a tangente dos ângulos do 2° e do 4° quadrantes é negativa.
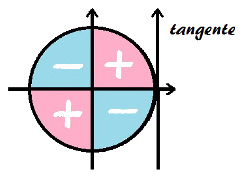
Variação do sinal da tangenteVamos agora analisar cada uma das afirmações:
I. tan 92° = –tan 88°
Reduzindo o ângulo de 92° ao primeiro quadrante, temos:
180° – 92° = 88°
Os ângulos de 92° e 88° são correspondentes e possuem tangente de mesmo módulo. De acordo com a figura, podemos constatar que o sinal das duas tangentes é diferente. Logo, a afirmação I é verdadeira.
II. tan 178° = tan 88°
Reduzindo o ângulo de 178° ao primeiro quadrante, temos:
180° – 178° = 2°
Os ângulos de 178° e 88° não são correspondentes, logo suas tangentes são diferentes. Assim sendo, a afirmação II é falsa.
III. tan 268° = tan 88°
Reduzindo o ângulo de 268° ao primeiro quadrante, temos:
268° – 180° = 88°
Os ângulos de 268° e 88° são correspondentes e possuem tangente de mesmo módulo. Através da figura, vemos que é igual o sinal de suas tangentes. Logo, a afirmação III é verdadeira.
IV. tan 272° = –tan 88°
Reduzindo o ângulo de 272° ao primeiro quadrante, temos:
360° – 272° = 88°
Os ângulos de 272° e 88° são correspondentes e suas tangentes possuem o mesmo módulo. Através da figura, vemos que é diferente o sinal de suas tangentes. Logo, a afirmação III é verdadeira.
São verdadeiras as afirmações I, III e IV. A alternativa correta é a letra d.