Exercícios sobre Resolução de Problemas com Sistemas de Equações
(VUNESP-04) Maria tem em sua bolsa R$15,60 em moedas de R$ 0,10 e de R$ 0,25. Dado que o número de moedas de 25 centavos é o dobro do número de moedas de 10 centavos, o total de moedas na bolsa é:
A) 68.
B) 75.
C) 78.
D) 81.
E) 84.
Seja x o número de moedas de R$ 0,10 e y o número de moedas de R$ 0,25. Portanto, se multiplicarmos 0,10 por x e adicionarmos ao produto de 0,25 por y, teremos o total de R$ 15,60, como a equação aponta:
0,10.x + 0,25.y = 15,60 (*)
A segunda informação no texto nos garante que y = 2.x. Resolvendo pelo método da substituição, substituiremos o valor encontrado para y em (*). Sendo assim:
0,10.x + 0,25.(2.x) = 15,60
0.10.x + 0,5 x = 15,60
0,6. x = 15,6
x = 26
Retornando à equação y = 2.x, vamos substituir o valor encontrado para x:
y = 2.x
y = 2.26
y = 52
Portanto, Maria tem 26 moedas de R$ 0,10 e 52 moedas de R$ 0,25. No total, Maria tem 78 moedas. A alternativa correta é a letra c.
(UNIFESP-04) Numa determinada livraria, a soma dos preços de aquisição de dois lápis e um estojo é R$10,00. O preço do estojo é R$5,00 mais barato que o preço de três lápis. A soma dos preços de aquisição de um estojo e de um lápis é:
a) R$3,00.
b) R$6,00.
c) R$12,00.
d) R$4,00.
e) R$7,00.
Seja l o preço de um lápis e e o preço de um estojo. Sabemos que se somarmos o preço de dois lápis com o de um estojo, teremos:
-
2.l + e = 10
Se o preço do estojo é R$5,00 mais barato que o preço de três lápis, podemos dizer que o valor de três lápis equivale ao preço de um estojo mais R$ 5,00, isto é:
-
3.l = e + 5
e = 3.l – 5
Utilizaremos novamente o método da substituição. Se e = 3.l – 5, substituiremos esse valor em 2.l + e = 10. Haverá, assim, a formação da seguinte equação:
2.l + 3.l – 5 = 10
5.l = 10 + 5
l = 15
5
l = 3
Portanto, o preço do lápis é R$ 3,00. Mas se o preço do estojo é dado por e = 3.l – 5, temos:
e = 3.3 – 5
e = 9 – 5
e = 4
O preço do estojo é R$ 4,00. Dessa forma, a aquisição de um estojo e de um lápis custará R$ 7,00. A alternativa correta é a letra e.
Em uma praça há 18 crianças andando de bicicleta ou de skate. No total, há 50 rodas girando pela praça. Quantas crianças andam de bicicleta e quantas andam de skate?
Nós não conhecemos o número de bicicletas e de skates que circulam pela praça, mas nós sabemos que a soma das bicicletas e dos skates é a mesma do total de crianças. Portanto, se chamarmos por b as bicicletas e por s os skates, teremos:
s + b = 18
Se há 50 rodas girando pela praça, podemos dizer que a soma das rodas das bicicletas e dos skates é 50. Vale lembrar que cada skate tem 4 rodas e cada bicicleta tem 2 rodas. Teremos uma nova equação em função das rodas:
4.s + 2.b = 18
Podemos formar o seguinte sistema de equações:
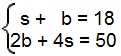
Agora, multiplicamos a primeira equação por menos 2, somando-a com a segunda:
– 2b – 2s = – 36
2b + 4s = 50
2s = 14
s = 14
2
s = 7
Então, nesse parque, há 7 skates. Resta-nos encontrar a quantidade de bicicletas. Para isso, utilizaremos a equação s + b = 18, na qual substituiremos o valor de skates encontrado:
s + b = 18
7 + b = 18
b = 18 – 7
b = 11
Portanto, nessa praça há 7 crianças andando de skate e 11 crianças andando de bicicleta.
A soma de dois números é 37. A diferença entre eles é 9. Quais são esses números?
Vamos identificar os números que procuramos como x e y. Vamos supor ainda que x > y. Temos então que x + y = 37 e x – y = 9.
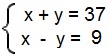
Utilizaremos o método da adição, somando as duas equações:
x + y = 37
x – y = 9
2x = 46
x = 46
2
x = 23
Substituindo esse valor em alguma das equações, teremos:
x + y = 37
y = 37 – x
y = 37 – 23
y = 14
Portanto, os números procurados são 23 e 14.
