Exercícios sobre retângulo
Um terreno no formato de um retângulo será utilizado para o plantio de duas culturas diferentes. Para realizar esse cultivo, a área será dividida em sua diagonal, logo, é necessário calcular o comprimento de uma das diagonais do retângulo. Sabendo que as suas dimensões são de 20 metros por 15 metros, o comprimento da sua diagonal é:
A) 22 metros.
B) 23 metros.
C) 24 metros.
D) 25 metros.
E) 26 metros.
Alternativa D.
Para encontrar a diagonal, basta utilizar o teorema de Pitágoras.
d² = h² + b²
d² = 20² + 15²
d² = 400 + 225
d² = 625
d = √625
d = 25
Em um retângulo, um lado é o triplo do outro. Sabendo que seu perímetro é igual a 64 cm, o valor do maior lado desse retângulo é de
A) 8 cm.
B) 24 cm.
C) 20 cm.
D) 16 cm.
E) 32 cm.
Alternativa B.
Seja x um lado do retângulo, e 3x o outro, então:
P = 2 · ( x + 3x)
P = 2 · (4x)
P = 8x
Sabemos que o perímetro é de 64 cm, logo:
8x = 64
x = 64 / 8
x = 8
Como o exercício pediu o maior lado, e sabemos que ele é igual ao triplo de 8, então ele mede:
8·3 = 24 metros
O pátio de uma escola tem formato retangular com 4 metros de largura e 5 metros de comprimento. Qual é a quantidade mínima de cerâmica retangular (de 5 centímetros por 10 centímetros) necessária para cobrir metade do pátio?
A) 4
B) 400
C) 200
D) 2000
E) 4000
Alternativa D.
Como as unidades de medidas estão diferentes, para saber quantas cerâmicas cabem no pátio primeiro vamos calcular a área em centímetros de cada um deles.
Área do pátio → Ap
4 m → 400 cm
5 m → 500 cm
Ap = b · h
Ap = 400 · 500 = 200.000 cm²
Já a área da cerâmica pode ser calculada por:
Área da cerâmica → Ac
Ac = b · h
Ac = 5 · 10
Ac = 50 cm²
O total de cerâmicas necessárias para cobrir todo o pátio pode ser calculada pela divisão:
200.000 : 50 = 4.000
Como somente a metade da área será coberta com cerâmica, então a quantidade necessária de cerâmicas é a metade de 4.000:
4.000 : 2 = 2.000
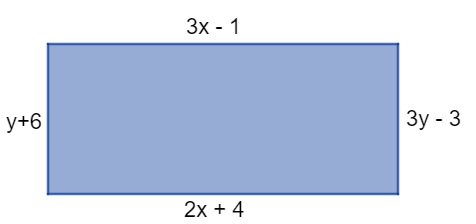
Analisando a imagem a seguir, podemos afirmar que x · y é igual a
A) 9,5
B) 12,5
C) 15,5
D) 20
E) 22,5
Alternativa E.
Em um retângulo os lados opostos são congruentes, logo, vamos igualar as equações que estão em lados opostos.
Analisando os lados horizontais:
3x – 1 = 2x + 4
3x – 2x = 4 + 1
x=5
Agora os lados verticais:
3y – 3 = y + 6
3y – y = 6 + 3
2y = 9
y = 9 / 2
y = 4,5
Agora basta calcular o produto entre x e y:
5 · 4,5 = 22,5
As medidas dos lados de um retângulo A são iguais ao dobro das medidas dos lados do retângulo B, então ao se comparar a área do retângulo A tem-se que ele é:
A) 2 vezes a área de B.
B) 4 vezes a área de B.
C) 6 vezes a área de B.
D) 8 vezes a área de B.
E) igual à área de B.
Alternativa B.
Seja b e h os lados do retângulo B, então sua área é:
AB = b · h = bh
Já o retângulo A possui lados medindo 2b e 2h, então sua área será:
AA = 2b · 2h = 4bh
Realizando a comparação, a área do retângulo A é 4 vezes a área do retângulo B.
A diferença entre a base e a altura de um terreno retangular é de 4 metros. Sabendo que a área ocupada por esse terreno é de 525 m², então o seu perímetro é igual a:
A) 273 metros
B) 52 metros
C) 46 metros
D) 184 metros
E) 92 metros
Alternativa E.
Seja x a base, então x – 4 é a altura.
Sabemos que:
A = b · h
A = x ( x – 4 )
x ( x – 4) = 525
x² – 4x = 525
x² – 4x – 525 = 0
Resolvendo a equação do 2º grau temos:
a = 1 b = – 4 e c = – 525
Δ = b² – 4ac
Δ = ( – 4) ² – 4 · 1 · ( – 525)
Δ = 16 + 2100
Δ = 2116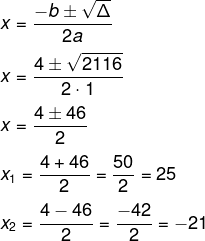
Como uma das soluções é negativa e não existe lado negativo, então x = 25 e x – 4 = 21. Assim, o perímetro é:
P = 2 · ( 25 + 21)
P = 2 · ( 46)
P = 92 m
(Enem 2017) A figura traz o esboço da planta baixa de uma residência. Algumas medidas internas dos cômodos estão indicadas. A espessura de cada parede externa da casa é 0,20 m e das paredes internas, 0,10 m
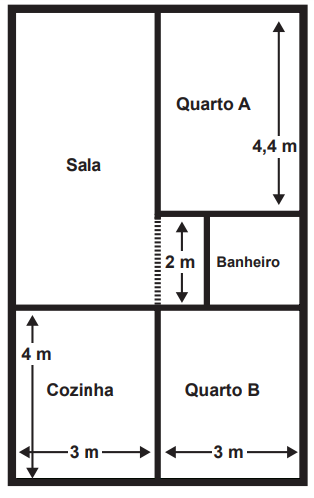
Sabe-se que, na localidade onde se encontra esse imóvel, o Imposto Predial Territorial Urbano (IPTU) é calculado conforme a área construída da residência. Nesse cálculo, são cobrados R$ 4,00 por cada metro quadrado de área construída. O valor do IPTU desse imóvel, em real, é
A) 250,00.
B) 250,80.
C) 258,64.
D) 276,48.
E) 286,00.
Alternativa E.
Note que o terreno todo é um retângulo, e o comprimento da base é igual ao comprimento da cozinha, mais o comprimento do quarto B, mais o comprimento de uma parede interna e de duas externas:
b = 3 + 3 + 0,1 + 0,2 + 0,2 = 6,5 metros
Já a altura é formada por duas paredes externas, a altura da cozinha, a altura do banheiro, a altura do quarto A e duas parentes internas:
0,2 + 0,2 + 4 + 2 + 4,4 + 0,1 + 0,1 = 11 metros
Então a área da casa é:
A = 11 · 6,5 = 71,5 m²
Como o valor cobrado é de 4 reais por metro quadrado, então:
71,5 · 4 = 286
Uma televisão de 32 polegadas tem largura igual a 73 centímetros. Sabendo que a área que ela ocupa é de 3.212 cm², qual é a medida da altura dessa televisão?
A) 36 cm
B) 34 cm
C) 40 cm
D) 44 cm
E) 42 cm
Alternativa D.
Como conhecemos sua largura e sua área, então:
c → comprimento
l → largura
A = c · l
3212 = 73c
c = 3212 / 73
c = 44
Sobre os retângulos, podemos afirmar que:
I – Todo retângulo é um paralelogramo;
II – Todo retângulo é um quadrado;
III – Todo retângulo é um quadrilátero.
As afirmativas são, respectivamente:
A) V, V, F
B) V, F, V
C) F, V, F
D) F, F, V
E) V, F, V
(IFG 2018) Na fase final da construção de um ginásio, um pedreiro necessita ladrilhar o chão que representa uma base retangular, cujas dimensões são 18 metros e 32 metros. Os ladrilhos utilizados são quadrados com 24 centímetros de lado. O número de ladrilhos necessários para revestir o espaço é de
A) 100.000.
B) 10.000.
C) 1.000.
D) 100.
Alternativa B.
Como a medida da cerâmica está em centímetros, para realizar a comparação entre a área do ginásio e a área dos ladrilhos, calcularemos a área do ginásio também em centímetros:
18 m → 1800 cm
32 m → 3200 cm
Ag = 1800 · 3200
Ag = 5.760.000
Al = 24 · 24 = 576
Realizando a divisão:
5.760.000 : 575 = 10.000
(IFG 2012) Em um retângulo, a razão entre a medida da altura e a medida da base é de 2/5 e, o perímetro desse retângulo mede 42 cm. A área desse retângulo em cm² é igual a:
A) 88
B) 90
C) 91
D) 94
E) 96
Alternativa B.
Seja 2x a altura e 5x a base, temos:
P = 2 ( 2x + 5x) = 42
4x + 10x = 42
14x = 42
x = 42 /14
x = 3
Então os lados medem:
2 · 3 = 6
5 · 3 = 15
6 · 15 = 90
Um retângulo possui diagonal medindo 30 cm, e base medindo 12 cm, então a sua altura em centímetros é igual a:
A) 24
B) 28
C) 30
D) 32
E) 36
Alternativa A.
Sabemos que:
d² = b² + h²
30² = 12² + h²
900 = 144 + h²
900 – 144 = h²
h² = 756
h = √756 = 24
