Exercícios sobre retas paralelas cortadas por uma transversal
Duas retas paralelas cortadas por uma transversal formam ângulos colaterais externos, cujas medidas, em graus, são dadas por 3x + 20° e 2x – 15°. Calcule a medida desses ângulos.
Se os ângulos são colaterais externos, sua soma resulta em 180°. Sendo assim, temos:
3x + 20° + 2x – 15° = 180°
5x + 5° = 180°
5x = 180° – 5°
5x = 175°
x = 175°
5
x = 35°
Tendo o valor de x conhecido, vamos agora identificar o valor dos ângulos:
3x + 20° = 3.35° + 20° = 105° + 20° = 125°
2x – 15° = 2.35° – 15° = 70° – 15° = 55°
Os ângulos procurados medem 55° e 125°.
Na figura a seguir, as retas r, s e t são paralelas e interceptadas por duas retas transversais u e v. Determine o valor do ângulo x.
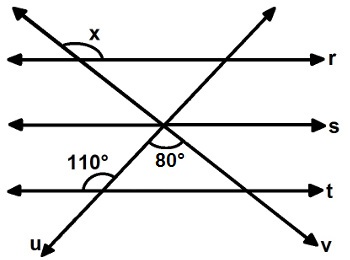
Retas r, s e t paralelas e interceptadas pelas retas transversais u e v
Analisando os ângulos formados pelas intersecções das retas paralelas com as transversais, podemos destacar um ângulo y suplementar ao ângulo de 110° e correspondente ao ângulo y', e z como o ângulo suplementar a x'. Veja na figura a seguir a representação dos ângulos x', y' e z:
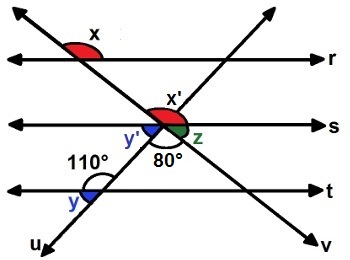
Análise dos ângulos da questão 2
Vamos identificar primeiro o valor de y, lembrando que ele é suplementar a 110°:
y + 110° = 180°
y = 180 – 110°
y = 70°
Mas como y = y', então y' = 70°. Vamos agora calcular o valor de z, sabendo que z + 80° + y' = 180°:
z + 80° + y' = 180°
z + 80° + 70° = 180°
z = 180° – 150°
z = 30°
Como já havíamos afirmado, x' e z são suplementares, logo:
x' + z = 180°
x' + 30 = 180°
x' = 180° – 30°
x' = 150°
Mas como x = x', podemos concluir que x = 150°.
(Cesgranio) As retas r e s da figura são paralelas cortadas pela transversal t. Se a medida do ângulo B é o triplo da medida do ângulo A, então B – A vale:
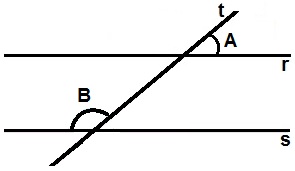
Retas r e s paralelas e interceptadas pela reta transversal t
a) 90°
b) 85°
c) 80°
d) 75°
e) 60°
Pela figura podemos identificar que existe um ângulo B' correspondente ao ângulo B tal que B' é suplementar a A, como podemos ver na figura a seguir:
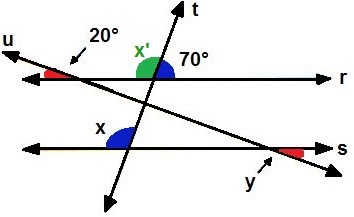
Análise dos ângulos da questão 3
Mas se B' e A são suplementares, podemos afirmar que B' + A = 180°. Mas se B' é correspondente a B, é correto afirmar que B + A = 180°, pois B' = B. De acordo com o enunciado, sabemos ainda que B = 3.A, sendo assim, temos:
B + A = 180°
3.A + A = 180°
4.A = 180°
A = 180°
4
A = 45°
Vamos agora determinar o valor de B:
B + A = 180°
B + 45° = 180°
B = 180° – 45°
B = 135°
Resta-nos identificar o valor de B – A:
B – A = 135° – 45° = 90°
Portanto, a alternativa correta é a letra a.
(UFG) Na figura abaixo as retas r e s são paralelas. A medida do ângulo b é:
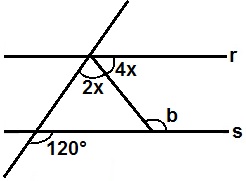
Retas r e s paralelas e interceptadas por retas transversais
a) 100°
b) 120°
c) 110°
d) 140°
e) 130°
Pela figura podemos notar que o ângulo 120° é correspondente à soma dos ângulos 2x e 4x. Sendo assim, temos:
2x + 4x = 120°
6x = 120°
x = 120°
6
x = 20°
Podemos ainda observar que os ângulos b e 4x são colaterais internos, isto é, a soma desses ângulos resulta em 180°, então:
b + 4.x = 180°
b + 4.20° = 180°
b + 80° = 180°
b = 180° – 80°
b = 100°
A alternativa correta é a letra a.
