Exercícios sobre retas perpendiculares
Duas retas são consideradas perpendiculares quando:
A) elas não possuem nenhum ponto em comum.
B) elas se interceptam formando um ângulo de 90°.
C) elas se interceptam possuindo dois pontos em comum.
D) elas pertencem ao mesmo plano.
Alternativa B
Duas retas são perpendiculares se o ângulo formado entre elas possui 90°.
Considere uma reta cuja equação geral é r: \(2x+3y-4=0\). A reta perpendicular a ela, representada por s, que passa pelos pontos (1, 1) possui equação geral igual a:
A) 3y – 2x + 1 = 0
B) x – y + 1 = 0
C) – 3y + 2x – 1 = 0
D) 2y – 3x + 1 = 0
E) 2y + 3x – 1 = 0
Alternativa D
Primeiramente, encontraremos o coeficiente angular da reta r:
\(2x+3y-4=0\ \)
\(3y=-\ 2x+4\)
\(y=\frac{-2x}{3}+\frac{4}{3}\)
Então, temos que \(m_r=-\ \frac{2}{3}\).
Sabemos que \(m_r\cdot m_s=-\ 1\):
\(-\frac{2}{3}m_s=-\ 1\)
\(m_s=-\ 1\cdot\left(-\frac{3}{2}\right)\)
\(m_s=\frac{3}{2}\)
Sabemos também que a equação reduzida da reta s é:
\(y=\frac{3}{2}x+n\)
Se x = 1 e y = 1:
\(1=\frac{3}{2}\cdot1+n\)
\(1=\frac{3}{2}+n\)
\(1-\frac{3}{2}=n\)
\(-\ \frac{1}{2}=n\)
A equação reduzida da reta é:
\(y=\frac{3}{2}x-\frac{1}{2}\)
Multiplicando por 2:
\(2y=3x-1\ \)
Igualando a zero:
\(2y-3x+1=0\)
Dadas as retas \(y_1=2x+3\) e \(y_2=-\frac{1}{2}x+8\), podemos afirmar que:
A) elas são paralelas.
B) elas são perpendiculares.
C) elas são coincidentes.
D) elas são reversas.
Alternativa B
Para analisar a posição relativa entre as retas, sabemos que os coeficientes angulares são \(m_1\) = 2 e \(m_2=-\frac{1}{2}\).
Caso as retas fossem paralelas ou coincidentes, os coeficientes angulares seriam os mesmos, o que não é o caso. Sendo assim, essas retas se interceptam. Verificaremos se elas são perpendiculares:
\(m_1\cdot m_2=-1\)
\(2\cdot\left(-\frac{1}{2}\right)=-1\)
\(-1=\ -1\ \)
Conclui-se, portanto, que as retas são perpendiculares.
(Cespe) Considere a reta r: y = –3(x – 2) e o ponto P = (3, 4). Considere, ainda, s a reta que passa por P e que é perpendicular à reta r. Com base nessas informações, assinale a opção que indica o ponto no qual se interceptam as retas r e s.
A) (9/10, 33/10)
B) (9, 12/10)
C) (3/8, 39/8)
D) (–9, –12)
E) (9/8, 33/8)
Alternativa A
A equação reduzida da reta r é:
y = – 3x + 6
Logo, sabemos que \(m_1=-\ 3\).
Como s é perpendicular à reta r, calcularemos o coeficiente angular da reta:
\(m_1\cdot m_2=-\ 1\)
\(-\ 3\cdot m_2=-\ 1\)
\(m_2=\frac{-\ 1}{-\ 3}\)
\(m_2=\frac{1}{3}\)
Como a reta passa pelo ponto P = (3, 4), temos que:
\(y\ =\ mx\ +\ n\)
\(y=\frac{1}{3}x+n\)
\(4=\frac{1}{3}\cdot3+n\)
\(4=1+n\)
\(4-1=n\)
\(n=3\)
Então, a equação da reta s é \(y=\frac{1}{3}x+3\).
Queremos o ponto em que as equações são iguais:
\(\frac{1}{3}x+3=-3x+6\)
\(\frac{1}{3}x+3x=6-3\)
\(\frac{10}{3}x=3\)
\(10x=3\cdot3\)
\(10x=9\)
\(x=\frac{9}{10}\)
Quando x = \(\frac{9}{10}\), temos que:
\(y=-\ 3x+6\)
\(y=-\ 3\cdot\frac{9}{10}+6\)
\(y=\frac{-27}{10}+6\)
\(y=\frac{33}{10}\)
Assim, o ponto em que as retas se encontram é:
\(\left(\frac{9}{10},\ \frac{33}{10}\right)\)
Sobre as retas perpendiculares, julgue as afirmativas a seguir:
I – Duas retas são ditas concorrentes quando elas são perpendiculares.
II – Quando as retas são perpendiculares, elas também são concorrentes.
III – Duas retas são paralelas quando elas formam um ângulo de 90° entre si.
Marque a alternativa correta:
A) Somente a afirmativa I está correta.
B) Somente a afirmativa II está correta.
C) Somente a afirmativa III está correta.
D) Todas as afirmativas são falsas.
Alternativa B
I – Falsa
Duas retas são concorrentes quando elas possuem um único ponto em comum.
II – Verdadeira
Para que duas retas sejam perpendiculares, é necessário que elas formem um ângulo de 90°.
III – Falsa
Duas retas são ditas paralelas se elas não possuem nenhum ponto em comum.
Analise as posições relativas entre as retas r e s e entre as retas t e p.
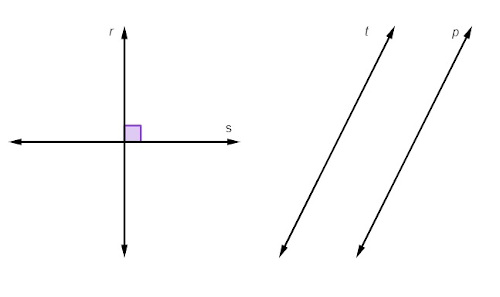
Podemos afirmar que elas são, respectivamente:
A) concorrentes, perpendiculares e coincidentes.
B) concorrentes, não perpendiculares e paralelas.
C) paralelas e concorrentes perpendiculares.
D) paralelas e coincidentes.
E) concorrentes, perpendiculares e paralelas.
Alternativa E
As retas r e s são concorrentes por se encontrarem em um único ponto. Além disso, o ângulo formado entre elas é um ângulo reto, logo r e s são retas perpendiculares. As retas t e p são paralelas, pois elas não possuem nenhum ponto em comum. Assim, as posições relativas entre as retas são, respectivamente, concorrentes, perpendiculares e paralelas.
A bissetriz dos quadrantes ímpares foi interceptada por uma reta de equação \(y=mx+n\) no ponto 2, 2. Sabendo que, além desse ponto, a reta passa pelo ponto (3, 1), o valor do seu coeficiente linear é:
A) 1
B) 2
C) 3
D) 4
E) 5
Alternativa D
A reta é perpendicular à bissetriz, e sabemos que a bissetriz possui equação y = x. Logo, o seu coeficiente é igual a 1.
O produto entre os coeficientes de duas retas perpendiculares é sempre igual a – 1, então podemos concluir que:
\(1\cdot m=-\ 1\)
\(m=-\ 1\ \)
Sendo m = – 1, temos que:
\(y=-\ x\ +\ n\)
Substituindo no ponto (3, 1):
\(1=-\ 3+n\)
\(n=1+3\ \)
\(n=4\ \ \)
As retas r: \(2x+4\) e s: – 3x + 1 foram representadas em um mesmo plano cartesiano. Analisando a representação, podemos afirmar que:
A) r e s são duas retas são paralelas.
B) r e s são duas retas coincidentes.
C) r e s são retas concorrentes e perpendiculares.
D) r e s são retas concorrentes, mas não perpendiculares.
E) r e s são retas relativamente reversas.
Alternativa D
Analisando a equação das retas, podemos afirmar que elas não são coincidentes nem paralelas, porque os coeficientes angulares são distintos. Logo, nos resta o fato de que essas retas são concorrentes, haja vista que os coeficientes angulares são distintos. Para verificar se essas retas são perpendiculares ou não, basta verificar se o produto entre os coeficientes angulares é \(-\ 1\):
\(m_1\cdot m_2=-\ 1\)
\(2\cdot(-\ 3)=-\ 6\)
Note que o produto entre os coeficientes angulares é diferente de 1. Sendo assim, podemos afirmar que essas retas são concorrentes, mas não perpendiculares.
Duas retas r e s se encontram no ponto P. Considere que A pertence à reta r e B pertence à reta s e que foi traçada a bissetriz PC do ângulo APB. Sabendo que r e s são perpendiculares, podemos afirmar que o ângulo suplementar do ângulo APC é igual a:
A) 45°
B) 60°
C) 75°
D) 120°
E) 135°
Alternativa E
Se as retas são perpendiculares, então elas formam entre si um ângulo reto. Logo, o ângulo APB possui 90°. A bissetriz AC divide esse ângulo ao meio, formando o ângulo APC, de 45°.
Queremos o ângulo suplementar a um ângulo de 45°, que é o ângulo de 180° – 45° = 135°.
Analise a imagem a seguir:
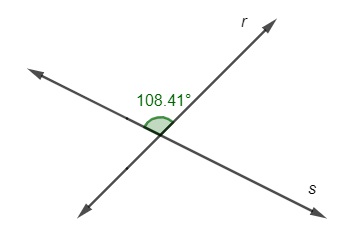
Sobre as retas r e s, podemos afirmar que:
I – As retas r e s são concorrentes.
II – As retas r e s são perpendiculares.
III – As retas r e s são paralelas.
Marque a alternativa correta:
A) Somente I é verdadeira.
B) Somente II é verdadeira.
C) Somente III é verdadeira.
E) Todas são verdadeiras.
Alternativa A
I – Verdadeira
Duas retas são concorrentes quando elas se encontram em um único ponto.
II – Falsa
As retas fazem um ângulo de 108°.
III – Falsa
As retas são concorrentes, logo elas não são paralelas.
(FEI) As retas 2x – y = 3 e 2x + ay = 5 são perpendiculares. Então:
A) a = – 1
B) a = 1
C) a = – 4
D) a = 4
E) n.d.a.
Alternativa D
Como as retas são perpendiculares, encontraremos o coeficiente angular da primeira:
\(-y=-\ 2x+3\ \ \)
Multiplicando por – 1:
\(y=2x-3\)
Agora, isolaremos o y na segunda equação:
\(ay=-\ 2x+5\)
\(y=\frac{-\ 2}{a}x+\frac{5}{a}\)
Para que as retas sejam perpendiculares, o produto entre os coeficientes angulares deve ser igual a – 1. O coeficiente angular da primeira é 2 e o da segunda é \( \frac{-\ 2}{a}\). Logo, temos que:
\(2\cdot\frac{-\ 2}{a}=-\ 1\)
\(\frac{-\ 4}{a}=-\ 1\)
\(-\ 4=-\ 1a\)
\(\frac{-\ 4}{-\ 1}=a\)
\(a=4\ \)
(Aeronáutica) As retas de equações y + x – 4 = 0 e 2y = 2x – 6 são, entre si,
A) paralelas.
B) coincidentes.
C) concorrentes e perpendiculares.
D) concorrentes e não perpendiculares.
Alternativa C
De início, encontraremos a equação reduzida de cada uma delas e, consequentemente, o coeficiente angular:
\(y=-\ x+4\ \)
Então, a primeira equação possui \(m=-\ 1\).
Analisando a segunda equação:
\(y=\frac{2}{2}x-\frac{6}{2}\)
\(y=x-3\ \)
Logo, na segunda equação, \(m=1\).
Como os coeficientes angulares são diferentes, essas retas são concorrentes. Agora, verificaremos se são perpendiculares.
Calculando o produto entre os coeficientes angulares:
\(-\ 1\cdot1=-\ 1\)
Isso mostra que essas retas são perpendiculares e concorrentes.
