Exercícios sobre Seno, Cosseno e Tangente
(UFPI) Um avião decola, percorrendo uma trajetória retilínea, formando com o solo um ângulo de 30° (suponha que a região sobrevoada pelo avião seja plana). Depois de percorrer 1.000 metros, a altura atingida pelo avião, em metros, é:
Interpretando a situação descrita no problema, temos a seguinte imagem que ilustra a situação em que a altura atingida pelo avião é dada por x:
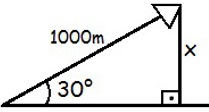
Representação da situação-problema da questão 1
Utilizando a fórmula para o cálculo do seno, temos:
sen 30° = x
1000
1 = x
2 1000
2x = 1000
x = 1000
2
x = 500 m
Portanto, o avião atingiu 500 m de altura.
(CEFET-MG - adaptado) Uma escada que mede 6m está apoiada em uma parede. Sabendo-se que ela forma com o solo um ângulo α e que
cos α = √5
3
a distância de seu ponto de apoio no solo até a parede, em metros, é:
Podemos ilustrar a situação descrita pelo enunciado do problema com a seguinte figura:
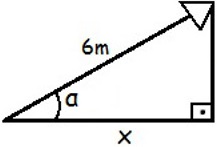
Representação da situação descrita na questão 2
Utilizando a fórmula para o cálculo do cosseno, temos:
cos ɑ = √5
3
cos ɑ = x
6
√5 = x
3 6
3x = 6.√5
x = 6.√5
3
x = 2√5
A distância do ponto de apoio até a parede é de aproximadamente 2√5 metros.
(U.F. Juiz de Fora – MG) Ao aproximar-se de uma ilha, o capitão de um navio avistou uma montanha e decidiu medir a sua altura. Ele mediu um ângulo de 30° na direção do seu cume. Depois de navegar mais 2 km em direção à montanha, repetiu o procedimento, medindo um novo ângulo de 45°. Então, usando √3 = 1,73, qual o valor que mais se aproxima da altura dessa montanha, em quilômetros?
Primeiramente, vamos visualizar a situação hipotética através do desenho abaixo:
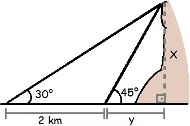
Representação da situação-problema da questão 3
Para resolver esse exercício, é preciso recordar que o cálculo da tangente é dado pelo quociente do cateto oposto pelo cateto adjacente e que, de acordo com a tabela trigonométrica dos ângulos notáveis, a tangente de 45° é 1 e a tangente de 30 é dada por √3. Sendo assim, temos:
3
tg 45° = x → x = tg 45°.y
y
tg 30° = x → x = tg 30°.(2+ y)
2 + y
Encontramos dois valores distintos para a variável x, igualando-os, temos:
tg 45° . y = tg 30° . (2 + y)
1. y = √3 . (2 + y)
3
y = 1,73 . (2 + y)
3
3y = 1,73y + 3,46
3 y – 1,73y = 3,46
1,27y = 3,46
y = 3,46
1,27
y = 2,7 km
Mas nós procuramos pelo valor correspondente a x, podemos então substituir o valor encontrado de y em alguma das equações destacadas em vermelho:
x = tg 45°. y
x = 1 . 2,7
x = 2,7 km
Portanto, a altura da montanha é de, aproximadamente, 2,7 quilômetros.
Determine os ângulos agudos de um triângulo retângulo de catetos que medem √3 cm e 1 cm.
Sejam os ângulos procurados a e b, temos então:
|
tg a = √3 tg a = √3 tg a = 60° |
tg b = 1 tg b = 1 . √3 tg b = √3 b = 30° |
Os ângulos agudos procurados são 30° e 60°.
Quando o Sol se encontra a 45º acima do horizonte, uma árvore projeta sua sombra no chão com o comprimento de 15 m. Determine a altura dessa árvore:
Para entender melhor a questão, é adequado tentar visualizar a situação do exercício. No desenho abaixo, o segmento de reta amarelo representa um raio solar que é o responsável por originar a sombra da árvore.
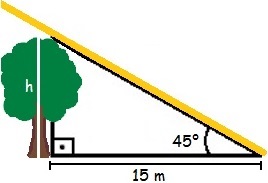
Esboço da situação problema da questão 5
Há um ângulo de 45° com o solo, e o comprimento da sombra é a base do triângulo. Pela tabela trigonométrica dos ângulos notáveis, verificamos que a tangente de 45° é 1. Utilizando a fórmula da tangente, temos:
tg 45° = h
15
h = 15 . tg 45°
h = 15 . 1
h = 15 m
Portanto, a altura dessa árvore é de 15 metros.
Determine os ângulos a e b, sabendo que a soma deles resulta em 90°.
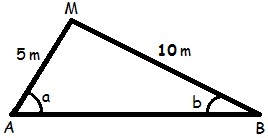
Figura do triângulo citado na questão 6
Se a + b = 90° e que a soma dos ângulos internos de um triângulo é 180°, podemos afirmar que o ângulo formado pelo vértice M é um ângulo reto (90°) e que a hipotenusa desse triângulo é o lado AB. Vamos então utilizar as relações fundamentais do triângulo retângulo.
tg a = cateto oposto = 10 = 2
cateto adjacente 5
tg b = cateto oposto = 5 = 0,5
cateto adjacente 10
Utilizando a tabela trigonométrica, verificamos facilmente que a = 63° e b = 27°.
