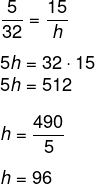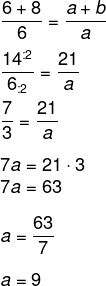Exercícios sobre teorema de Tales
Estes exercícios testarão seus conhecimentos sobre o teorema de Tales, que demonstra proporcionalidade entre certos segmentos de retas.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Sobre o teorema de Tales, marque a alternativa que o define corretamente.
A) Dado um triângulo retângulo, a soma do quadrado dos catetos é sempre igual ao quadrado da hipotenusa.
B) Se um polinômio p(x) possui grau n, então o número de raízes complexas que esse polinômio pode admitir é igual a n.
C) Um feixe de retas paralelas determina sobre duas retas transversais segmentos proporcionais.
D) Dado um triângulo qualquer, a soma dos seus ângulos internos é sempre igual a 180º e a dos externos é igual a 360º.
Alternativa C.
A alternativa que define corretamente o enunciado do teorema de Tales é a alternativa C.
-
Questão 2
Analise a imagem a seguir:
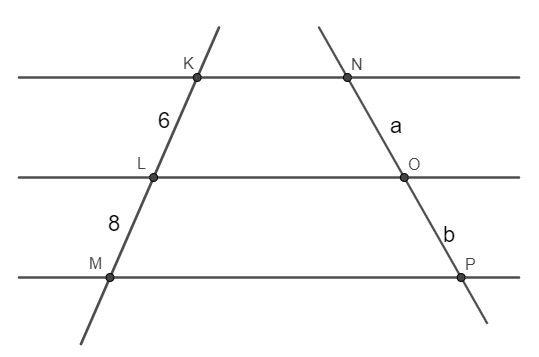
Sabendo que a + b = 21, então o valor de a é respectivamente igual a:
A) 9
B) 10
C) 11
D) 12
E) 14
-
Questão 3
Sobre o triângulo ABC foi traçado o segmento de reta DE, conforme a imagem a seguir.
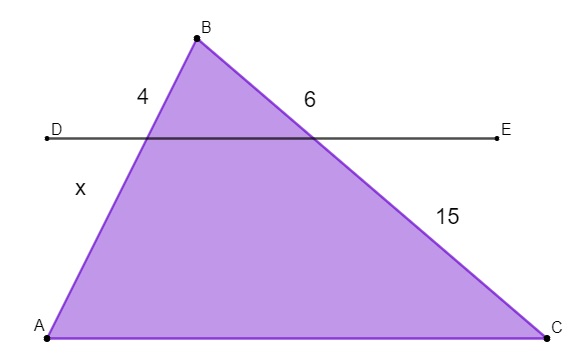
Sabendo que o segmento DE é paralelo à base AC do triângulo, então podemos afirmar que x é igual a:
A) 9,5
B) 8,0
C) 9,0
D) 9,5
E) 10,0
Alternativa E.
Montando as proporções, temos que:
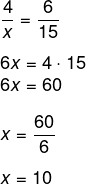
-
Questão 4
Sabendo que as retas r, s e t são paralelas e analisando a imagem, podemos afirmar que x é igual a aproximadamente:
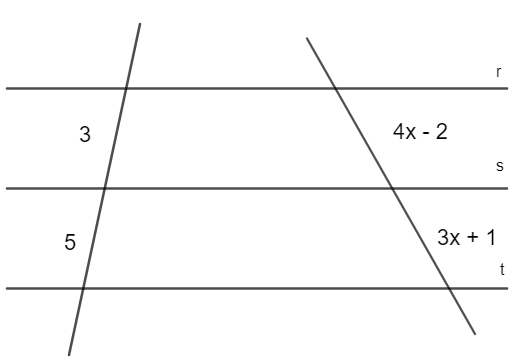
A) 1,10
B) 1,18
C) 1,20
D) 1,25
E) 1,29
Alternativa B.
Para encontrar o valor de x, basta montar as proporções:
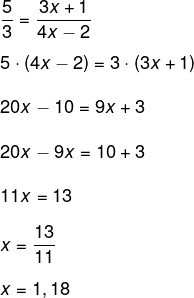
-
Questão 5
Na imagem a seguir, está representado um triângulo com as suas medidas dadas em centímetros:

Sabendo que AC//DE e que AB = 21 cm, então b mede:
A) 11
B) 12
C) 13
D)14
E) 15
Alternativa D.
Montando a proporção, temos que:
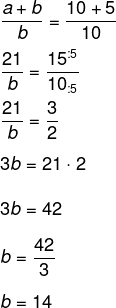
-
Questão 6
(Sociesc) Um pinheiro de 7,2 m projeta uma sombra de 11,2 m. Dois passarinhos pousam nessa árvore, um bem no topo e outro um pouco mais abaixo. Se a distância entre as sombras que esses passarinhos projetam no chão é de 4,2 m, qual é a distância entre os dois passarinhos?
A) 3,2 m
B) 2,2 m
C) 2,5 m
D) 2,7 m
E) 3,7 m
Alternativa D
Seja x a distância entre os passarinhos, calculando as proporções, temos que:
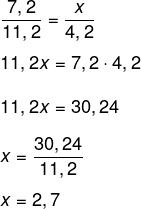
-
Questão 7
Sabendo que as retas r, s e t são paralelas, então o comprimento de x, em centímetros, é igual a:
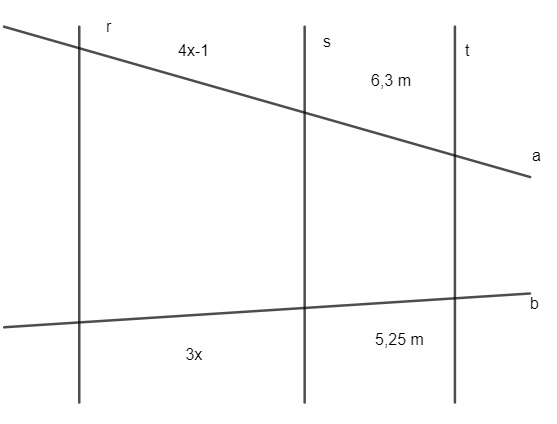
A) 2,0
B) 2,5
C) 3,0
D) 3,4
E) 3,5
Alternativa B.
Para encontrar o valor de x, basta montar as proporções:
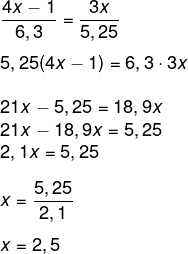
-
Questão 8
(Conspass – 2018) Um condomínio foi projetado de modo que do portão principal saem duas alamedas não paralelas entre si e transversais às demais ruas de circulação, que formam um feixe de paralelas. Abaixo apresentamos um desenho simplificado dessa situação:
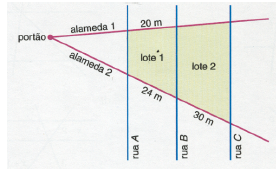
Qual o comprimento da lateral do lote 2 que fica voltada para a alameda 1?
A) 25 metros
B) 24 metros
C) 20 metros
D) 30 metros
E) 26 metros
Alternativa A.
Seja x a medida da lateral do lote 2, então:
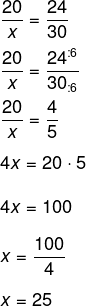
-
Questão 9
(Enem - 2009) A rampa de um hospital tem na sua parte mais elevada uma altura de 2,2 metros. Um paciente ao caminhar sobre a rampa percebe que se deslocou 3,2 metros e alcançou uma altura de 0,8 metro. A distância em metros que o paciente ainda deve caminhar para atingir o ponto mais alto da rampa é
A) 1,16 metro.
B) 3,0 metros.
C) 5,4 metros.
D) 5,6 metros.
E) 7,04 metros.
Alternativa D
Para compreender melhor a situação, convém fazer a representação geométrica da rampa:
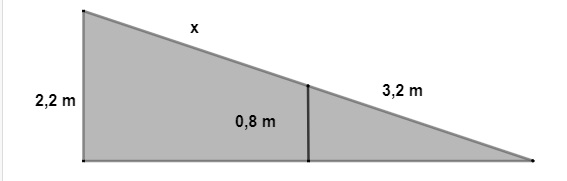
Seja x +3,2 m o comprimento total da rampa, temos que:
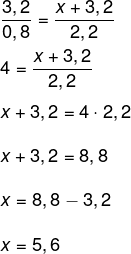
-
Questão 10
Sabendo que as retas na horizontal são paralelas, a medida do segmento AC é igual a?
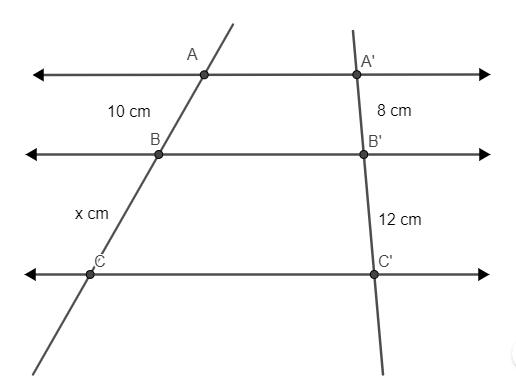
A) 10 cm
B) 15 cm
C) 25 cm
D) 28 cm
E) 30 cm
Alternativa C.
Montando as proporções:
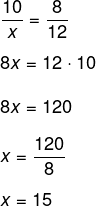
Como queremos o comprimento de AC, basta realizar a soma 15 + 10 = 25 cm.
-
Questão 11
(Fuvest–SP) Três terrenos têm frente para a rua A e para a rua B, como na figura. As divisas laterais são perpendiculares à rua A. Qual a medida de x, y e z em metros sabendo que a frente total para essa rua tem 180 m?
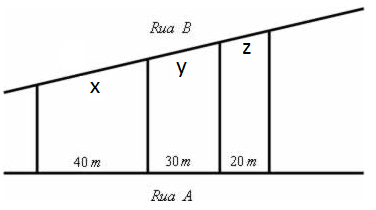
A) 90, 60 e 30
B) 40, 60 e 90
C) 80, 60 e 40
D) 20 30 e 40
Alternativa C.
Sabemos que x + y + z = 180. Analisando a rua 1, temos que 40 + 30 + 20 = 90.
Note que o comprimento na rua B é o dobro do comprimento na rua A, então: 180 : 90 = 2.
Sendo 2 a razão de proporção, temos que:
x = 2 · 40 = 80
y = 2 · 30 = 60
z = 2 · 20 = 40
-
Questão 12
Para realizar a medição de um prédio, Marcelo decidiu utilizar o teorema de Tales. Ele decidiu observar a sombra que o prédio projetava e a sombra de um poste cuja altura já era conhecida por Marcelo. Ele realizou as medições conforme a imagem a seguir:
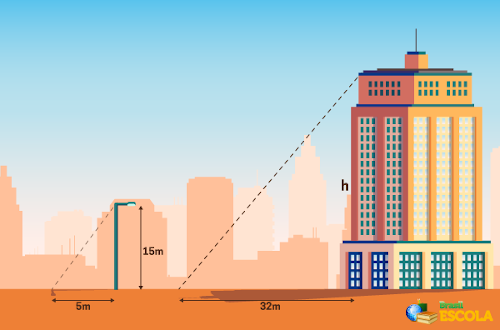
Sabendo que o feixe de luz solar incide de forma paralela sobre o prédio e o poste, então podemos afirmar que a altura h do prédio mede:
A) 90 m
B) 92 m
C) 94 m
D) 96 m
E) 98 m
Alternativa D.
Montando as razões, temos que: