Exercícios sobre tronco de pirâmide
Essa lista de exercícios te ajudará a verificar o seu aprendizado sobre tronco de pirâmide, com questões contendo os principais conceitos que envolvem esse tema.
Publicado por: Raul Rodrigues de OliveiraQuestões
-
Questão 1
Um reservatório possui o formato de tronco de pirâmide, com 10 metros de altura e 2 bases quadradas com 6 metros e 4 metros. O volume desse reservatório é aproximadamente igual a:
A) 253 m³
B) 250 m³
C) 247 m³
D) 242 m³
E) 239 m³
Alternativa A
Calculando a área das bases, temos o seguinte:
A1 = 4² = 16 m²
A2 = 6² = 36 m²
Assim, calcula-se:
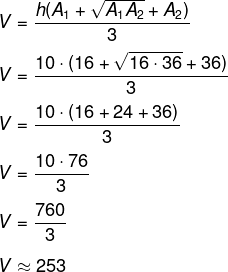
-
Questão 2
Na busca por um vaso para colocar uma muda de jabuticaba, Poliana encontrou vários formatos diferentes de sólidos geométricos, entre eles, os que estão na imagem a seguir.
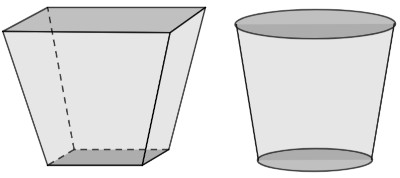
O nome dos sólidos geométricos que eles representam são, respectivamente,
A) trapézio e cilindro.
B) tronco de prisma e cone.
C) prisma e tronco de cilindro.
D) tronco de pirâmide e tronco de cone.
E) cubo e prisma de base circular.
Alternativa D
Podemos constatar que há dois sólidos que são, respectivamente, um tronco de pirâmide e um tronco de cone.
-
Questão 3
(EsPCEx 2009). Um reservatório em forma de tronco de pirâmide regular de base quadrada e dimensões indicadas na figura deverá ter suas paredes laterais externas cobertas por uma tinta impermeável, cujo rendimento é de 11m² por galão.
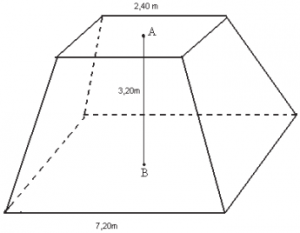
O número mínimo de galões que devem ser adquiridos para tal operação é:
A) 6
B) 7
C) 9
D) 10
E) 11
Alternativa B
Para calcular a área lateral, primeiramente deve-se calcular a geratriz do lado, que nada mais é que a altura do trapézio.
g² = (L/2 – l/2)² + h²
g² = (3,6 – 1,2)² + 3,2²
g² = 2,4² + 3,2²
g² = 10,24 + 5,76
g² = 16
g = √16
g = 4
Calculando a área do trapézio, tem-se o seguinte:
-
B = 7,2
-
b = 2,4
-
h = 4
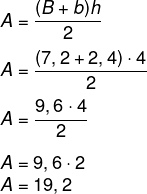
Como há 4 trapézios, a área lateral é igual a 19,2 · 4 = 76,8 m².
Sabemos que cada galão pinta 11 m², então 76,8 : 11 = 6,98, sendo necessário um total de 7 galões.
-
-
Questão 4
Uma pirâmide regular que possui 12 cm de altura foi seccionada por um plano paralelo à base, formando um tronco de pirâmide com metade da altura desta. Sabendo que sua base maior mede 18 cm, a área total do tronco de pirâmide é de:
A) 598 cm²
B) 651 cm²
C) 727 cm²
D) 810 cm²
E) 930 cm²
Alternativa D
De início, encontraremos a altura do tronco de pirâmide.
Sabemos que 1/2 de 12 é igual a 12:2 = 6 cm.
Como a altura foi divida por 3, a aresta do lado menor também será 1/3 da aresta do lado maior, ou seja:
18 : 2 = 9 cm
Logo, a área da base menor é igual a:
Ab = 9² = 81 cm²
Calculando a área da base maior, obtém-se:
AB = 18² = 324
Calculando a altura da face lateral, temos que:
g² = h² + (L/2 – l/2)²
g² = h² + (9 – 4,5)²
g² = 6² + 4,5²
g² = 36 + 20,25
g² = 56,25
g = √56,25
g = 7,5
Calculando a área lateral, sabe-se que ela é composta por 4 trapézios, em que:
-
B = 18
-
b = 9
-
g = h = 7,5
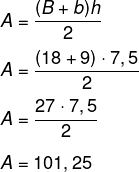
Como há 4 trapézios na área lateral, calcula-se:
Al = 101,25 · 4
Al = 405 cm²
Portanto, a área total é a soma da área da base maior, área da base menor e área lateral:
AT = 81 + 324 + 405 = 810 cm²
-
-
Questão 5
Um sólido geométrico foi seccionado por um plano paralelo à sua base formando outros dois sólidos, como mostra a imagem a seguir:
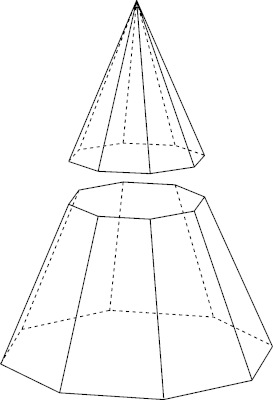
Analisando o sólido geométrico formado pela parte inferior, pode-se afirmar que se trata de um(a)
A) prisma de base octogonal.
B) pirâmide de base octogonal.
C) tronco de cone de base octogonal.
D) tronco de pirâmide de base octogonal.
E) paralelogramo de base octogonal.
Alternativa D
Quando é feita uma secção transversal em uma pirâmide, na parte inferior obtém-se um tronco de pirâmide. Como a base da pirâmide era octogonal, o tronco de pirâmide é octogonal.
-
Questão 6
A seguir, está representada a planificação de um poliedro.
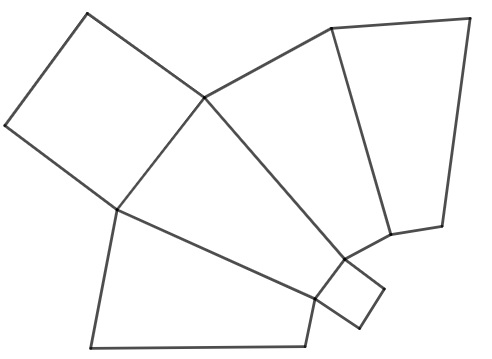
Analisando a imagem, pode-se afirmar que ela é a planificação de um(a)
A) prima de base trapezoidal.
B) prisma de base quadrada.
C) pirâmide de base trapezoidal.
D) pirâmide de base quadrada.
E) tronco de pirâmide de base quadrada.
Alternativa E
Note que há duas bases quadradas, mas com lados de medidas diferentes, ou seja, são quadrados semelhantes. As faces laterais são formadas por trapézios, uma característica do tronco de pirâmide de base quadrada.
-
Questão 7
Um reservatório de água tem o formato de um tronco de pirâmide com altura de 6 cm. As áreas das suas bases são 36 cm² e 64 cm². Sabendo que 25% desse reservatório está ocupado, o volume de água que ainda cabe nesse reservatório é de:
A) 296 cm³
B) 222 cm³
C) 252 cm³
D) 104 cm³
E) 74 cm³
Alternativa B
Como já conhecemos as áreas, primeiramente calcularemos o volume:
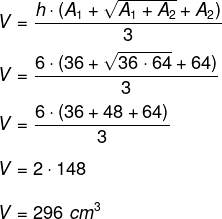
Sabemos que 25% do reservatório está ocupado, restando 75% a ser ocupado. Sendo assim, o volume restante é de 296 ⸳ 0,75 = 222 cm³.
-
Questão 8
Em uma indústria serão fabricadas embalagens no formato de tronco de pirâmide com base quadrada, sendo que a base menor possui lados que medem 20 cm e a maior, lados que medem 30 cm. Qual deve ser a altura dessa embalagem para que o seu volume seja igual a 22800 cm³?
A) 22 cm
B) 25 cm
C) 28 cm
D) 36 cm
E) 40 cm
Alternativa D
Sendo h a altura, temos que:
A1 = 20² = 400
A2 = 30² = 900
Substituindo na fórmula do volume, calcula-se o seguinte:
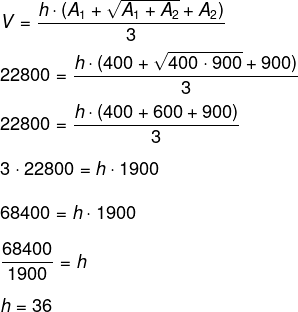
Portanto, a altura deve ser de 36 cm.
-
Questão 9
(UFRGS) Considere a planificação do sólido formado por 2 faces quadradas e por 4 trapézios congruentes, conforme medidas indicadas na figura representada abaixo.
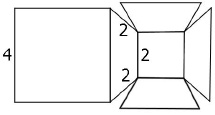
O volume desse sólido é
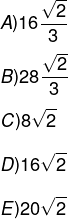
Alternativa B
Analisando a planificação, é possível perceber que ela pertence a um tronco de pirâmide com base quadrada.
Calculando a área de sua base maior e de sua base maior, obtém-se o seguinte:
A1 = 2² = 4
A2 = 4² = 16
Para encontrar a altura, deve-se traçar o trapézio que passa pela diagonal das bases, sabendo que a diagonal de um quadrado é igual a l√2. Dessa forma, as diagonais vão medir 2√2 e 4√2.
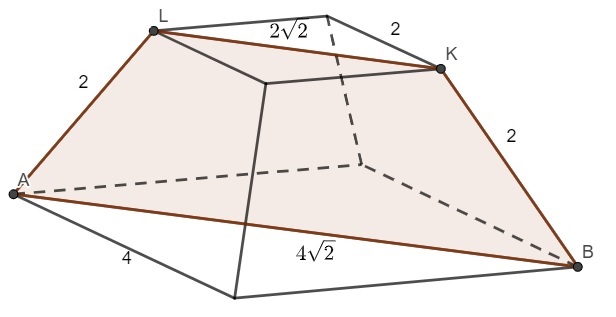
Analisando o trapézio que formamos ao ligar os vértices ABKL, é possível encontrar sua altura pelo teorema de Pitágoras.
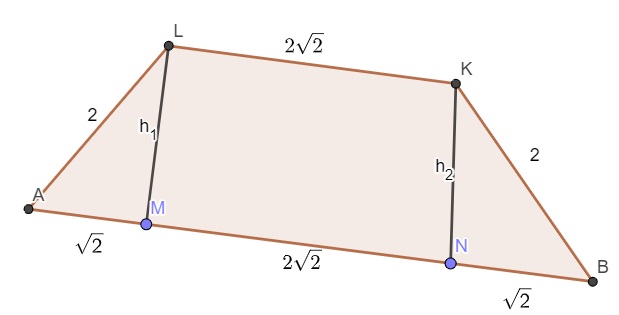
Calculando a altura, temos que:
2² = h² + √2²
4 = h² + 2
4 – 2 = h²
2 = h²
h = √2
Sabendo que a altura do tronco é √2, é possível calcular o seu volume:
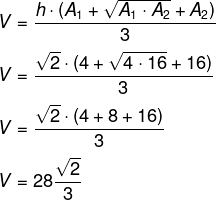
-
Questão 10
Sobre o tronco de pirâmide, julgue as afirmativas a seguir:
I → Ele pode ser obtido pela secção meridional da pirâmide.
II → Ele é formado por duas bases formadas por polígonos semelhantes e faces laterais no formato de trapézio.
III → Sempre possui base quadrada.
Marque a alternativa correta:
A) Somente I é verdadeira.
B) Somente II é verdadeira.
C) Somente III é verdadeira.
D) Todas são falsas
Alternativa B
-
I → Falsa. A secção dve ser transversal, e não meridional.
-
II → Verdadeira.
-
III → Falsa. Assim como a pirâmide, a sua base pode ser qualquer polígono.
-
-
Questão 11
(Enem 2009) Uma fábrica produz velas de parafina em forma de pirâmide quadrangular regular com 19 cm de altura e 6 cm de aresta da base. Essas velas são formadas por 4 blocos de mesma altura — 3 troncos de pirâmide de bases paralelas e 1 pirâmide na parte superior —, espaçados de 1 cm entre eles, sendo que a base superior de cada bloco é igual à base inferior do bloco sobreposto, com uma haste de ferro passando pelo centro de cada bloco, unindo-os, conforme a figura.
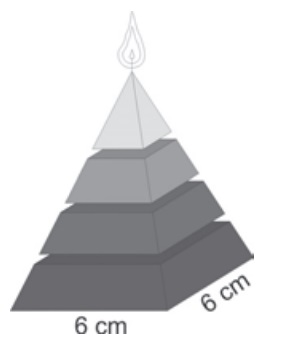
Se o dono da fábrica resolver diversificar o modelo, retirando a pirâmide da parte superior, que tem 1,5 cm de aresta na base, mas mantendo o mesmo molde, quanto ele passará a gastar com parafina para fabricar uma vela?
A) 156 cm³
B) 189 cm³
C) 192 cm³
D) 216 cm³
E) 540 cm³
Alternativa B
Sabendo que há 1 cm de distância entre os blocos, a altura da pirâmide maior é de 19 – 3 = 16 cm.
A pirâmide maior possui 6 cm de lado da base. Como a base é um quadrado, então A b = l² = 6² = 36.
Calculando o volume da pirâmide maior, obtém-se o seguinte:
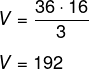
A altura da pirâmide menor na parte superior é de 16 : 4 = 4. A aresta é de 6 : 4 = 1,5. Então, a área da base da pirâmide menor é de 1,5² = 2,25. Calculando o volume:
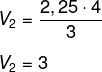
Por fim, basta calcular a diferença entre os volumes: 192 – 3 = 189.
-
Questão 12
(Enem 2020) Uma das Sete Maravilhas do Mundo Moderno é o Templo de Kukulkán, localizado na cidade de Chichén Itzá, no México. Geometricamente, esse templo pode ser representado por um tronco reto de pirâmide de base quadrada.
As quantidades de cada tipo de figura plana que formam esse tronco de pirâmide são:A) 2 quadrados e 4 retângulos.
B) 1 retângulo e 4 triângulos isósceles.
C) 2 quadrados e 4 trapézios isósceles.
D) 1 quadrado, 3 retângulos e 2 trapézios retângulos.
E) 2 retângulos, 2 quadrados e 2 trapézios retângulos.
Alternativa C
Vejamos a representação de um tronco de pirâmide de base quadrada.
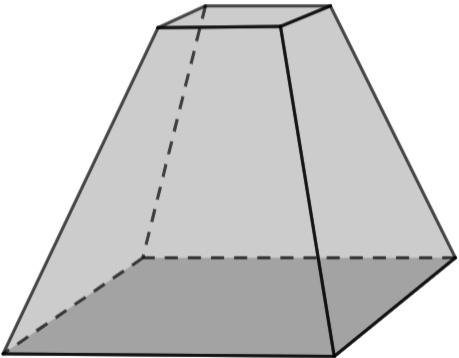
Analisando esse sólido geométrico, é possível perceber que as suas bases (face superior e face inferior) são formadas cada uma por 1 quadrado.
Há 4 faces laterais, todas no formado de trapézio. Como as arestas que formam os lados oblíquos dos trapézios são congruentes, há 4 trapézios isósceles. Portanto, há 2 quadrados e 4 trapézios isósceles.