Exercícios sobre Meia-vida
Meia-vida ou período de semidesintegração é o tempo para que metade dos núcleos radioativos se desintegre, ou seja, o tempo para que uma amostra radioativa se reduza à metade.
Publicado por: Jennifer Rocha Vargas FogaçaQuestões
-
Questão 1
O criptônio-89 possui o tempo de meia-vida igual a 3,16 minutos. Dispondo-se de uma amostra contendo 4,0 . 1023 átomos desse isótopo, ao fim de quanto tempo restarão 1,0 . 1023 átomos?
Alternativa “b”.
A cada 3,16 minutos, a quantidade de átomos cairá pela metade. Assim, para chegar a um quarto da quantidade inicial, serão necessários dois períodos de meia-vida, ou seja: 3,16 + 3,16 = 6,32 minutos.
4,0 . 1023 átomos → 3,16 minutos → 2,0 . 1023 átomos→ 3,16 minutos → 1,0 . 1023 átomos
-
Questão 2
O césio-137 possui meia-vida de 30 anos. Se tivermos 12 g desse elemento, após quanto tempo essa massa será reduzida para 0,75 g?
Alternativa “d”
12g → 6g → 3g → 1,5g → 0,75g
30 anos 30 anos 30 anos 30 anosSerão necessários 120 anos para que essa amostra de césio-137 reduza-se a 0,75 g.
-
Questão 3
Após 12 dias, uma substância radioativa tem a sua atividade reduzida para 1/8 da inicial. A meia-vida dessa substância será de:
Alternativa “b”.
A atividade ou velocidade de desintegração é proporcional à massa. Assim, ao final de 12 dias, teremos:
mfinal = 1 minicial
8Abaixo temos a fórmula da expressão geral usada para calcular a massa (mfinal) existente após x meias-vidas:
mfinal = minicial
2xAssim, podemos escrever:
minicial = minicial
8 2x
1 = 1
8 2x
1 = 1
23 2x
x = 3Portanto, as meias-vidas transcorridas em 12 dias são 3. Para determinar a duração de cada meia-vida, aplicamos uma regra de três:
3 meias vidas --------- 12 dias
1 meia-vida ----------- y
y = 1 . 12 dias
3y = 4 dias.
-
Questão 4
(Vunesp-SP) Em Goiânia, 100 g de 137CsCℓ foram liberados de uma cápsula, antes utilizada em radioterapia, e causaram um grave acidente nuclear. O gráfico representa a cinética de desintegração desse isótopo.
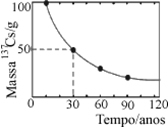
Para o 137Cs, o tempo de meia-vida e o tempo para que 87,5% tenha se desintegrado são, em anos, respectivamente:
Alternativa ‘d’.
Pelo gráfico concluímos que o tempo de meia-vida é de 30 anos.
100 – 87,5 = 12,5%
100% → 50% → 25% → 12,5%
30 anos 30 anos 30 anosO tempo para que 87,5% da amostra tenha se desintegrado é de 90 anos.
-
Questão 5
(FESP-SP) Bomba de cobalto é um aparelho muito usado na radioterapia para tratamento de pacientes, especialmente portadores de câncer. O material radioativo usado nesse aparelho é o 2760Co, com um período de meia-vida de aproximadamente 5 anos.
Admita que a bomba de cobalto foi danificada e o material radioativo exposto à população. Após 25 anos, a atividade deste elemento ainda se faz sentir num percentual, em relação à massa inicial, de:
Alternativa ‘a’.
100% x → 5 anos → 50% x → 5 anos → 25% x → 5 anos → 12,5% x → 5 anos → 6,25% x → 5 anos → 3,125% x
5 . 5 = 25 anos.
-
Questão 6
(UFPR) O polônio-210 é um emissor alfa com um tempo de meia-vida de 138 dias. Supondo que se coloquem, em um recipiente fechado, 21g desse isótopo, ficando retidas, no recipiente, as partículas alfas que capturarão elétrons, transformando-se em hélio, teremos, ao fim de 276 dias, uma massa de hélio igual a (He-4):
Alternativa ‘d’.
A massa inicial de polônio é de 21 g, e o seu número de mol é dado por:
__21g___ = 0,1 mol
210 g/mol0,1 mol de Po → após 138 dias → 0,05 mol de Pó → após 138 dias → 0,025 mol de Po
276 diasO número de mol de Po que se desintegrou é igual a 0,075 mol, que originou 0,075 mol de hélio.
1 mol de He -------- 4g
0,075 mol de He --- x
x = 0,30 g de He