Exercícios sobre Função de 2º Grau
Calcule o valor de k de modo que a função f(x) = 4x² – 4x – k não tenha raízes, isto é, o gráfico da parábola não possui ponto em comum com o eixo x.
∆ < 0
b² – 4ac < 0
(–4)² – 4 * 4 * (–k) < 0
16 + 16k < 0
16k < – 16
k < –1
O valor de k para que a função não tenha raízes reais deve ser menor que – 1.
Determine os valores de m, para que a função f(x) = (m – 2)x² – 2x + 6 admita raízes reais.
Para essa situação temos que ∆ ≥ 0.
∆ ≥ 0
b² – 4ac ≥ 0
(–2)² – 4 * (m – 2) * 6 ≥ 0
4 – 4 * (6m – 12) ≥ 0
4 – 24m + 48 ≥ 0
– 24m ≥ – 48 – 4
– 24m ≥ – 52
24m ≤ 52
m ≤ 52/24
m ≤ 13/6
O valor de m que satisfaça a condição exigida é m ≤ 13/6.
(Vunesp-SP)
O gráfico da função quadrática definida por y = x² – mx + (m – 1), em que m Є R, tem um único ponto em comum com o eixo das abscissas. Determine y associado ao valor de x = 2.
Um ponto em comum significa dizer uma única raiz, então ∆ = 0.
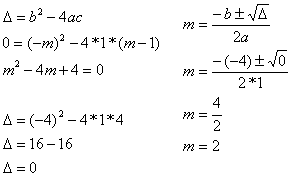
y = x² – mx + (m – 1)
Substituir m = 2, no intuito de obter a lei da função
y = x² – 2x + (2 – 1)
y = x² – 2x +1
Substituindo x = 2, para determinarmos o valor de y
y = 2² – 2 * 2 + 1
y = 4 – 4 + 1
y = 1
Temos que a equação possui a lei de formação y = x² – 2x +1. E quando x = 2, o valor de y se torna igual a 1.
(UCSal-BA)
Determine os pontos de intersecção da parábola da função f(x) = 2x² – 3x + 1, com o eixo das abscissas.
No instante em que a parábola cruza o eixo das abscissas o valo de y ou f(x) é igual a zero. Portanto:
f(x) = 0
2x² – 3x + 1 = 0
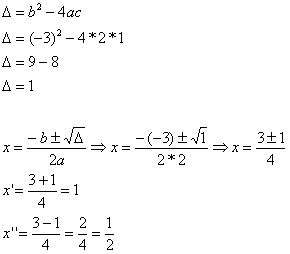
Os pontos de interseção são:
x = 1 e y = 0
x = 1/2 e y = 0






