Exercícios sobre Números Binomiais
Na resolução de exercícios sobre números binomiais, aplicamos o binômio de Newton para determinar quaisquer elementos do desenvolvimento dos binômios.
Publicado por: Amanda Gonçalves RibeiroQuestões
-
Questão 1
Qual é o 6° termo do desenvolvimento do binômio de Newton (a – 1)6?
Se desejamos saber o 6° termo do binômio de Newton, consideramos k = 5, n = 6, x = a e y = – 1. Logo:
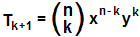
T5 + 1 =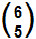
.a6 – 5.(– 1)5T6 = 6! .a1.(– 1)
5! (6 – 5)!T6 = 6 . 5! .a.(– 1)
5!. 1!T6 = – 6.a5
Portanto, o sexto termo do desenvolvimento do binômio (a – 1)6 é – 6.a5.
-
Questão 2
Determine o termo médio (ou central) no desenvolvimento do número binomial (a – 2)9.
Considerando que o primeiro termo é (a – 2)0, sabemos que esse binômio possui dez termos. Logo precisamos determinar o 5° termo, isto é, estamos procurando T5. Para tanto, temos k = 4, n = 9, x = a e y = – 2.
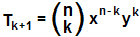
T4 + 1 =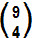
.a9 – 4.(– 2)4T5 = 9! .a5. 24
4! (9 – 4)!T5 = 9 . 8 . 7 . 6 . 5! .a5. 16
(4. 3 . 2 .1). 5!T5 = 9 . 8 . 7 . 6 .a5. 16
24T5 = 48384.a5
24T5 = 2016.a5
O termo central do número binomial (a – 2)9 é 2016.a5.
-
Questão 3
(FGV) A soma dos coeficientes do desenvolvimento de (2x+ y)5 é igual a:
Para determinar a soma dos coeficientes do desenvolvimento de binômios como esse, basta considerar x = 1 e y = 1. Dessa forma, teremos:
(2x + y)5 = (2.1 + 1)5 = (3)5 = 243
O valor encontrado de 243 corresponde exatamente à soma dos coeficientes de (2x + y)5, portanto, a alternativa correta é a letra c.
-
Questão 4
(FEI) A soma de todos os coeficientes do desenvolvimento de (14x – 13y)237 é:
Para determinar a soma dos coeficientes do desenvolvimento de um número binomial, não é necessário utilizar a fórmula-padrão do binômio de Newton, basta considerar as variáveis como 1, isto é, basta fazer x = 1 e y = 1. Dessa forma, teremos:
(14x – 13y)237 = (14.1 – 13.1)237 = (14 – 13)237 = 1237 = 1
Sendo assim, podemos identificar que a soma dos coeficientes de (14x – 13y)237 é 1. Logo, a alternativa correta é a letra b.