Exercícios sobre aceleração
(FPS) Um automóvel percorre uma rodovia com velocidade inicialmente constante igual a 80 km/h. O motorista do veículo avista um radar e reduz sua velocidade para 60 km/h, percorrendo nesse trajeto uma distância igual a 20 m. O módulo da desaceleração sofrida pelo automóvel nesse percurso foi de aproximadamente:
A) 5,4 m/s²
B) 7,5 m/s²
C) 2,5 m/s²
D) 11 m/s²
E) 15 m/s²
Alternativa A.
Primeiramente, converteremos as velocidades de km/h para m/s:
\(\frac{80}{3,6}≅22,22\ m/s\)
\(\frac{60}{3,6}≅16,66\ m/s\)
Calcularemos a desaceleração através da fórmula de Torricelli:
\(v_f^2=v_i^2+2\cdot a\cdot ∆x\)
\(16,66^2=22,22^2+2\cdot a\cdot 20\)
\(277,77=493,82+40\cdot a\)
\(277,77-493,82≅40\cdot a\)
\(-216,05≅40\cdot a\)
\(a≅-\frac{216,05}{40}\)
\(a≅-5,40\ m/s^2 \)
(Unesp) Um foguete lançador de satélites, partindo do repouso, atinge a velocidade de 5400 km/h após 50 segundos. Supondo que esse foguete se desloque em trajetória retilínea, sua aceleração escalar média é de
A) 30 m/s².
B) 150 m/s².
C) 388 m/s².
D) 108 m/s².
E) 54 m/s².
Alternativa A.
Primeiramente, converteremos a velocidade de km/h para m/s:
\(\frac{5400\ km/h}{3,6}=1500\ m/s\)
Calcularemos a aceleração média através da sua fórmula:
\(a_m=\frac{∆v}{∆t}\)
\(a_m=\frac{1500}{50}\)
\(a_m=30\ m/s^2 \)
(Uern) Veja o gráfico da velocidade em função do tempo de um corpo em movimento retilíneo uniformemente variado representado abaixo.
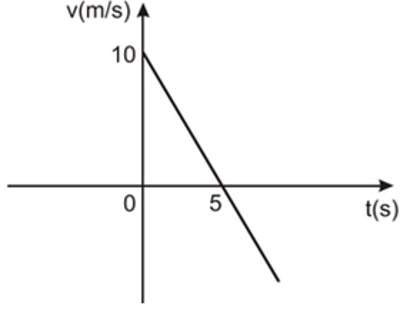
Considerando a posição inicial desse movimento igual a 46 m, então a posição do corpo no instante t = 8 s é
A) 54 m.
B) 62 m.
C) 66 m.
D) 74 m.
Alternativa B.
Primeiramente, calcularemos a aceleração desse corpo, através da fórmula da aceleração média:
\(a_m=\frac{∆v}{∆t}\)
\(a_m=\frac{v_f-v_i}{t_f-t_i}\)
\(a_m=\frac{0-10}{5-0}\)
\(a_m=-\frac{10}5\)
\(a_m=-2\ m/s^2\)
Então, calcularemos a distância final através da equação da função horária da posição no movimento retilíneo uniformemente variado:
\(x_f=x_i+v_i\cdot t+\frac{a\cdot t^2}2\)
\(x_f=46+10\cdot 8+\frac{-2\cdot 8^2}2\)
\(x_f=46+80+\frac{-2\cdot 64}2\)
\(x_f=46+80-64\)
\(x_f=62\ m\)
(FMTM) Um cientista, estudando a aceleração média de três diferentes carros, obteve os seguintes resultados:
O carro I variou sua velocidade de v para 2v em um intervalo de tempo igual a t.
O carro II variou sua velocidade de v para 3v em um intervalo de tempo igual a 2t.
O carro III variou sua velocidade de v para 5v em um intervalo de tempo igual a 5t.
Sendo, respectivamente, a1, a2 e a3 as acelerações dos carros I, II e III, pode-se afirmar que:
A) \(a_1=a_2=a_3\)
B) \(a_1>a_2>a_3\)
C) \(a_1<a_2<a_3\)
D) \(a_1=a_2>a_3\)
E) \(a_1=a_2<a_3\)
Alternativa D.
Calcularemos a aceleração média de cada um dos veículos, através da sua fórmula:
\(a_m=\frac{∆v}{∆t}\)
\(a_m=\frac{v_f-v_i}{t_f-t_i}\)
- Carro 1:
\(a_1=\frac{∆v}{∆t}\)
\(a_1=\frac{v_f-v_i}{t_f-t_i}\)
\(a_1=\frac{2v-v}t\)
\(a_1=\frac{v}t\)
- Carro 2:
\(a_2=\frac{∆v}{∆t}\)
\(a_2=\frac{v_f-v_i}{t_f-t_i}\)
\(a_2=\frac{3v-v}{2t}\)
\(a_2=\frac{2v}{2t}\)
\(a_2=\frac{v}t\)
- Carro 3:
\(a_3=\frac{∆v}{∆t}\)
\(a_3=\frac{v_f-v_i}{t_f-t_i}\)
\(a_3=\frac{5v-v}{5t}\)
\(a_3=\frac{4v}{5t}\)
\(a_3=0,8\cdot \frac{v}t\)
Então, \(a_1=a_2>a_3\)
Qual é a aceleração de um carro que estava inicialmente parado e atingiu uma velocidade de 70 m/s em 5 s?
A) \(13\ m/s^2\)
B) \(14\ m/s^2\)
C) \(15\ m/s^2\)
D) \(16\ m/s^2\)
E) \(17\ m/s^2\)
Alternativa B.
Calcularemos a aceleração do carro através da equação da função horária da velocidade no movimento retilíneo uniformemente variado:
\(v_f=v_i+a\cdot t\)
\(70=0+a\cdot 5\)
\(70=a\cdot 5\)
\(\frac{70}5=a\)
\(14\ m/s^2=a\)
O deslocamento angular final da roda de uma bicicleta é de 300 radianos. Sabendo que ela levou 60 segundos para completar esse deslocamento partindo do repouso, determine qual foi a aceleração aproximada sofrida pela roda.
A) \(0,16\ rad/s^2\)
B) \(0,20\ rad/s^2\)
C) \(0,24\ rad/s^2\)
D) \(0,28\ rad/s^2\)
E) \(0,32\ rad/s^2\)
Alternativa A.
Calcularemos a aceleração através da equação da função horária da posição no movimento circular uniformemente variado (MCUV):
\(φ_f=φ_i+ω_i\cdot t+\frac{α\cdot t^2}2\)
Como ele partiu do repouso, tanto a sua velocidade angular quanto deslocamentos iniciais serão nulos:
\(300=0+0\cdot 60+\frac{α\cdot 60^2}2\)
\(300=\frac{α\cdot 3600}2\)
\(300=α\cdot 1800\)
\(α=\frac{300}{1800}\)
\(α≅0,16\ rad/s^2\)
Considerando que a massa da Terra é de \(5,972\cdot 10^{24}\ kg\) e que o seu raio médio é 6.371 km, calcule a aceleração da gravidade da Terra sobre um corpo que está na superfície do planeta.
Dado: considere a constante de gravitação universal como \(6,67\cdot 10^{-11}\ N.m^2/kg^2\).
A) \(8,69\ m/s^2 \)
B) \(9,78\ m/s^2 \)
C) \(9,80\ m/s^2 \)
D) \(9,98\ m/s^2 \)
E) \(10,0\ m/s^2 \)
Alternativa C.
Primeiramente, converteremos o raio médio de quilômetros para metros:
\(6.371\ km=6371000\ m=6,371\cdot 10^6\ m\)
Calcularemos a aceleração da gravidade da Terra sobre um corpo que está na superfície do planeta através da fórmula da aceleração da gravidade na superfície do planeta ou um corpo celeste:
\(g=\frac{G\cdot m}{r^2 }\)
\(g=\frac{6,7\cdot 10^{-11}\cdot 5,972\cdot 10^{24}}{(6,371\cdot 10^6)^2} \)
\(g=\frac{40,0124\cdot 10^{-11+24}}{40,589641\cdot 10^{12}}\)
\(g=\frac{40,0124\cdot 10^{13}}{40,589641\cdot 10^{12}}\)
\(g=0,985778613\cdot 10^{13-12}\)
\(g=0,985778613\cdot 10^1\)
\(g=9,85778613\)
\(g≈9,8\ m/s^2 \)
Qual foi a aceleração angular média da roda de um motociclista que se movia com velocidade angular de 1,2 rad/s durante 3 segundos?
A) \(0,1\ rad/s^2\)
B) \(0,2\ rad/s^2\)
C) \(0,3\ rad/s^2\)
D) \(0,4\ rad/s^2\)
E) \(0,5\ rad/s^2\)
Alternativa C.
Calcularemos a aceleração angular média através da sua fórmula:
\(α_m=\frac{∆ω}t\)
\(α_m=\frac{1,2}4\)
\(α_m=0,3\ rad/s^2\)
Dentre as opções abaixo, qual não se trata de um tipo de aceleração?
A) Aceleração angular.
B) Aceleração centrípeta.
C) Aceleração da gravidade.
D) Aceleração tangencial.
E) Aceleração elástica.
Alternativa E.
Existem diversos tipos de aceleração, como a aceleração angular, a aceleração centrípeta, a aceleração das cargas, a aceleração da gravidade, a aceleração média e a aceleração tangencial, mas a aceleração elástica não é um desses tipos.
Uma pessoa corre com uma velocidade de 14,4 km/h ao redor de uma praça circular com 200 metros de raio. A partir dessas informações, qual a aceleração centrípeta do corredor?
A) \(0,16\ m/s^2\)
B) \(0,24\ m/s^2\)
C) \(0,32\ m/s^2\)
D) \(0,40\ m/s^2\)
E) \(0,48\ m/s^2\)
Alternativa A.
Primeiramente, converteremos a velocidade de km/h para m/s:
\(\frac{14,4 km/h}{3,6}=4\ m/s\)
Calcularemos a aceleração centrípeta do corredor através da fórmula da aceleração centrípeta:
\(a_{CP}=\frac{v^2}R\)
\(a_{CP}=\frac{4^2}{100}\)
\(a_{CP}=\frac{16}{100}\)
\(a_{CP}=0,16\ m/s^2 \)
Sabendo que o raio médio do planeta Marte é \(3,4\cdot 10^6\ m\) e a sua massa é de \(6,4\cdot 10^{23}\ kg\), calcule qual a aceleração da gravidade sofrida por um corpo que está distante 10.000 metros da superfície de Marte.
Dados: \(G = 6,67\cdot 10^{-11}\ N.m^2/kg^2\).
A) \(0,82\ m/s^2 \)
B) \(1,69\ m/s^2 \)
C) \(2,47\ m/s^2 \)
D) \(3,68\ m/s^2 \)
E) \(4,25\ m/s^2 \)
Alternativa D.
Calcularemos a aceleração da gravidade para o corpo que está distante de Marte através da fórmula da aceleração da gravidade para corpos externos ao planeta ou um corpo celeste:
\(g=\frac{G\cdot m}{(r+h)^2}\)
\(g=\frac{6,7\cdot 10^{-11}\cdot 6,4\cdot 10^{23}}{(3,4\cdot 10^6+10\ 000)^2}\)
\(g=\frac{42,88\cdot 10^{12}}{(3\ 410\ 000)^2}\)
\(g=\frac{42,88\cdot 10^{12}}{11\ 628\ 100\ 000\ 000}\)
\(g≅3,68\cdot 10^{-12}\cdot 10^{12}\)
\(g≅3,68\ m/s^2 \)
Quais das alternativas apresentam as unidades de medida correspondentes às grandezas físicas estudadas na aceleração?
I. A aceleração é medida em metros por segundo.
II. A velocidade é medida em metros por segundo.
III. O tempo é medido em metros.
IV. A distância é medida em metros.
V. A altura é medida em metros por segundo ao quadrado.
A) Alternativas I e II.
B) Alternativas III e IV.
C) Alternativas I e V.
D) Alternativas II e III.
E) Alternativas II e IV.
Alternativa E.
I. A aceleração é medida em metros por segundo. (incorreta)
A aceleração é medida em metros por segundo ao quadrado.
II. A velocidade é medida em metros por segundo. (correta)
III. O tempo é medido em metros. (incorreta)
O tempo é medido em segundos.
IV. A distância é medida em metros. (correta)
V. A altura é medida em metros por segundo ao quadrado. (incorreta)
A altura é medida em metros.
